Mechanika: pohyb telesa
Každé teleso môže byť buď v pokoji (nehýbe sa), alebo v pohybe (hýbe sa). Pokoj a pohyb sú však relatívne pojmy, teda nevieme jednoznačne povedať, či je v teleso v pokoji alebo v pohybe (napríklad keď sedím v aute a nehýbem sa, ale auto sa pohybuje, som v pokoji alebo v pohybe?). Stav musíme určiť vždy vzhľadom na niečo. Keď sedím v aute a nehýbem sa, ale auto sa pohybuje, som v pokoji vzhľadom na auto, ale v pohybe vzhľadom na cestu a okolitú krajinu. Keď sedím na zemi a nehýbem sa, tak som v pokoji vzhľadom na Zem, ale v pohybe vzhľadom na slnko a ostatné planéty.
Hmotný bod je bod telesa, ktorým nahrádzame skutočné teleso, aby sme mohli určiť jeho polohu. Zanedbávame pri ňom rozmery telesa, ale nie jeho hmotnosť. Trajektória je čiaru, po ktorej sa pohybuje (ktorú pri pohybe opíše) vybraný bod telesa (hmotný bod). Dráha (s) je dĺžka trajektórie. Je to fyzikálna veličina so značkou s a jednotkou (rovnako ako pri dĺžke, keďže dráha je vlastne dĺžka) meter (m). Pri akomkoľvek pohybe (či teleso zrýchľuje alebo spomaľuje, či sa pohybuje dopredu alebo dozadu...) narastá a v pokoji sa nemení, nikdy nemôže klesať.
Delenie pohybu:
- Základné delenie pohybu je na posuvný pohyb (pri ktorom za daný čas všetky body telesa prejdú rovnakú trajektóriu) a otáčavý pohyb (pri ktorom za daný čas opíšu všetky body telesa okrem bodov na osi otáčania rovnaký uhol)
- Podľa tvaru trajektórie na priamočiary pohyb a krivočiary pohyb
- Podľa rýchlosti na rovnomerný pohyb (za rovnaké časové úseky prejde rovnakú dráhu) a nerovnomerný pohyb (za rovnaké časové úseky prejde rôznu dráhu; jeho osobitné druhy sú zrýchlený pohyb a spomalený pohyb)
Pohyb telesa najčastejšie opisujeme pomocou grafov (väčšinu pomocou grafov závislosti dráhy od času).
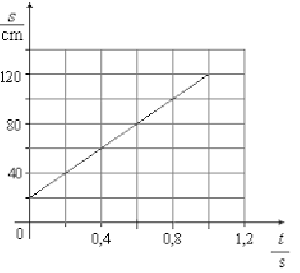
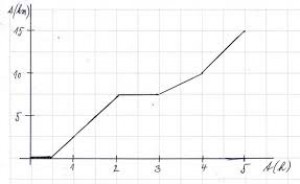
| Grafom rovnomerného pohybu je priamka. | Grafom nerovnomerného pohybu je krivka. |
|
|
Vidíme, že hoci je grafom krivka, vždy ide smerom hore alebo je vodorovná, nikdy neklesá. To je preto, že dráha tiež nikdy nemôže klesať. |
Rýchlosť pohybu
Rýchlosť (v) je dráha prejdená za jednotku času. Je to vektorová fyzikálna veličina so značkou v. Vypočítame ju tak, že dráhu, ktorú teleso prešlo, vydelíme časom, za ktorý ju prešlo. Vzorec na jej výpočet je teda v=s/t. Hlavná jednotka rýchlosti je meter za sekundu (m/s alebo m/s,alebo m•s-1), ale ďalšia používaná jednotka je kilometer za hodinu (km/h alebo km/h alebo km•h-1). Ako tieto jednotky premieňať? Skúsme to odvodiť:
|
Odvoďme si jednotku km/h z hlavnej jednotky m/s: Vieme, že meter premeníme na kilometer tak, že ho vydelíme 1000 a sekundu na hodinu tak, že ju vydelíme 3600 (hodina sa skladá zo 60 minút, minúta zo 60 sekúnd a 60•60=3600). Získame zložený zlomok, ktorý upravíme. |
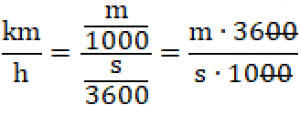 |
| Získame teda vzťah v ktorom platí, že kilometer za hodinu získame tak, že meter za sekundu vynásobíme 3,6. | 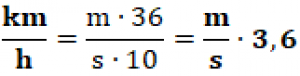 |
| Keďže pri premene z m/s na km/h sme násobili 3,6, tak pri opačnom procese (čiže premene z km/h na m/s) budeme deliť 3,6. | 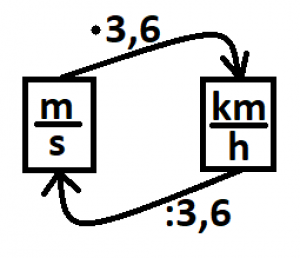 |
Rýchlosť rovnomerného pohybu sa nemení, čiže počas celého pohybu je konštantná.
Rýchlosť nerovnomerného pohybu sa mení, čiže nevieme vyjariť "rýchlosť nerovnomerného pohybu". Vieme však vyjadriť tzv. okamžitú rýchlosť (rýchlosť v určitom čase, napríklad rýchlosť, ktorú vidíme na tachometri) a priemernú rýchlosť, ktorú počítame tak, že celkovú dráhu vydelíme celkovým časom. POZOR! PRIEMERNÚ RÝCHLOSŤ NEPOČÍTAME TAK, AKO SA POČÍTA KLASICKÝ ARITMETICKÝ PRIEMER (ČIŽE VYDELENÍM OKAMŽITÝCH RÝCHLOSTI V RÔZNYCH OKAMIHOCH POČTOM DANÝCH OKAMIHOV)! Aj to by sa dalo, ale pohyb by sme museli rozdeliť na nekonečne veľa častí, čiže by sme mali nekonečne veľa okamžitých rýchlostí. Na toto potrebujeme špeciálne matematické operácie (limity, derivácie, integrály), ktoré sú však veľmi náročné a učia sa až na vysokej škole.
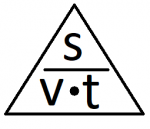 Keďže rýchlosť vypočítame vydelením dráhy časom, tak pomocou rovnice si vieme odvodiť, že dráhu vypočítame vynásobením rýchlosti časom a čas vydelením dráhy rýchlosťou. Ako pomôcku vieme teda využiť trojuholníkový vzorec, podobne ako pri hustote. Toto platí pri pre rovnomerný pohyb aj pre nerovnomerný pohyb (pri nerovnomernom pohybe dosadzujeme do vzorca priemernú, nie okamžitú rýchlosť).
Keďže rýchlosť vypočítame vydelením dráhy časom, tak pomocou rovnice si vieme odvodiť, že dráhu vypočítame vynásobením rýchlosti časom a čas vydelením dráhy rýchlosťou. Ako pomôcku vieme teda využiť trojuholníkový vzorec, podobne ako pri hustote. Toto platí pri pre rovnomerný pohyb aj pre nerovnomerný pohyb (pri nerovnomernom pohybe dosadzujeme do vzorca priemernú, nie okamžitú rýchlosť).
Vyrieš príklady (riešenia sú na konci príspevku):
1.) Autíčko sa pohybuje 4 sekundy rovnomerným pohybom rýchlosťou 2m/s. Akú dráhu prejde?
2.) Cyklista prešiel dráhu 10km za 25 minút. Aká bola jeho priemerná rýchlosť? Vyjadrite to v kilometroch za hodinu aj v metroch za sekundu.
Zložitejšie príklady na rovnomerný pohyb (napríklad kedy a kde sa stretnú dve telesá s rôznou rýchlosťou) sa riešia pomocou rovníc. Opisujem to v príspevku Lineárne rovnice a slovné úlohy riešené pomocou nich.
Niečo navyše
Pohrajme sa s grafmi
Niekedy kreslíme nielen graf závislosti dráhy od času, ale aj graf závislosti rýchlosti od času.
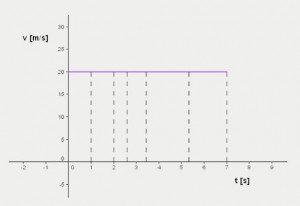
| Grafom rovnomerného pohybu vodorovná priamka, keďže rýchlosť je stále rovnaká. | Grafom nerovnomerného pohybu je krivka alebo priamka, ktorá nie je vodorovná. |
 |
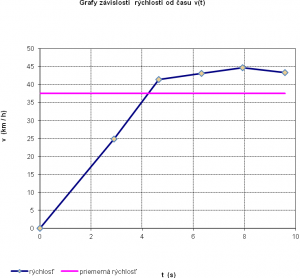 |
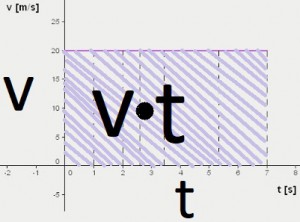 Z takýchto grafov sa dá vypočítať dráha rovnomerného, ale aj nerovnomerného pohybu. Ale ako? Odvoďme si to pomocou rovnomerného pohybu. Na základe vzorca vieme, že dráha rovnomerného pohybu sa počíta ako súčin rýchlosti a času. Keď sa ale pozrieme na graf, vidíme, že vlastne počítame obsah obdĺžnika pod čiarou grafu.
Z takýchto grafov sa dá vypočítať dráha rovnomerného, ale aj nerovnomerného pohybu. Ale ako? Odvoďme si to pomocou rovnomerného pohybu. Na základe vzorca vieme, že dráha rovnomerného pohybu sa počíta ako súčin rýchlosti a času. Keď sa ale pozrieme na graf, vidíme, že vlastne počítame obsah obdĺžnika pod čiarou grafu.
Odvodili sme teda, že dráha sa rovná obsahu plochy pod krivkou (priamkou) grafu závislosti rýchlosti od času.
Aplikujme to teda na nerovnomerný pohyb:
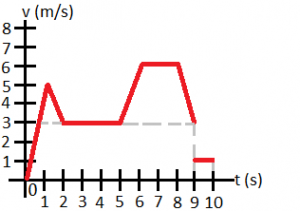
|
Výpočet: Sivými prerušovanými čiarami som plochu pod krivkou rozdelil na nám známe geometrické útvary (dole pravouhlý lichobežník, vľavo hore trojuholník, vpravo hore lichobežník a vpravo od dolného lichobežníka štvorec), ktorým viem vypočítať obsahy. Súčet týchto obsahov nám dá dráhu.
obsah dolného lichobežníka = (dolná základna + horná základna) • výška / 2 = (9s+(9s-1s))•3m•s-1/2=17
obsah trojuholníka = (strana • výška na ňu) / 2 = ((2s-1s)•(5m•s-1-3m•s-1)/2=(1
obsah horného lichobežníka = (dolná základňa + horná základňa) • výška / 2 = ((9s-5s)+(8s-6s))•(6m•s-1-3m•s-1)/2=(6
obsah štvorca = dĺžka • šírka = 1
Spočítame obsahy: s=25,5m+1m+9m+1m=36,5m Vypočítame priemernú rýchlosť: v=s/t=36,5m/10s=3,65m/s=13,14km/h
Odpoveď: Dráha telesa je 36,5m a jeho priemerná rýchlosť je 3,65m/s, čiže 13,14km/h. |
Dráhu aj priemernú rýchlosť vieme spočítať aj keď má plocha pod krivkou zložitejší tvar. Počíta sa to pomocou integrálov. To je však zložitá matematická operácia, ktorá sa učí používať až na vysokej škole. Takže ak to chcete vedieť, choďte študovať na MATFYZ![]() .
.
Rovnomerne zrýchlený pohyb (pohyb s konštantným zrýchlením)
Špeciálnym druhom nerovnomerného pohybu je rovnomerne zrýchlený pohyb (lepší termín je pohyb s konštantným zrýchlením). Rýchlosť pri ňom narastá (alebo klesá) rovnomerne (lineárne), čiže grafom závislosti rýchlosti od času je priamka.
Aby sme vedeli riešiť úlohy s rovnomerne zrýchleným pohybom, potrebujeme zaviesť ďalšiu fyzikálnu veličinu - zrýchlenie (a). Je to tiež vektorová veličina, rovnako ako rýchlosť alebo sila. Má rovnaký smer ako rýchlosť a samotný pohyb. Vypočítame ho tak, že zmenu rýchlosti vydelíme časom. Vzorec na výpočet zrýchlenia teda je a=Δv/t=v-v0/t. v0 v tomto vzorci vyjadruje počiatočnú rýchlosť. Pomocou rovnice si vieme z tohto vzorca odvodiť vzorce na výpočet rýchlosti (v=a•t+v0), počiatočnej rýchlosti (v0=v-a•t), času (t=Δv/a=v-v0/a) a zmeny rýchlosti (Δv=a•t). Jednotka zrýchlenia je meter za sekundu na druhú (m/s2 , čiže m•s-2)
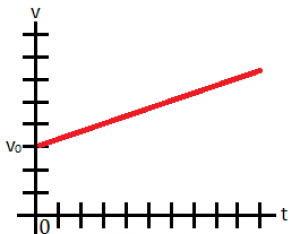
 Graf závislosti rýchlosti od času sa bude začínať (keď sa pýtame na os y) v hodnote počiatočnej rýchlosti. Pokiaľ je počiatočná rýchlosť 0, tak sa aj graf, samozrejme, bude začínať v nule.
Graf závislosti rýchlosti od času sa bude začínať (keď sa pýtame na os y) v hodnote počiatočnej rýchlosti. Pokiaľ je počiatočná rýchlosť 0, tak sa aj graf, samozrejme, bude začínať v nule.
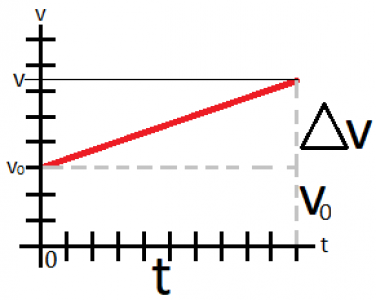
Pokúsme sa z grafu odvodiť vzorec na výpočet dráhy: vieme, že dráha sa rovná obsahu plochy pod krivkou (priamkou) grafu. Graf rovnomerne zrýchleného pohybu sa skladá z obdĺžnika a pravouhlého trojuholníka. Obdĺžnik má dĺžku rovnú času (t) a výšku rovnú počiatočnej rýchlosti (v0). Jeho obsah teda bude v0•t. Trojuholník bude mať dĺžku rovnú času (t) výšku rovnú rozdielu rýchlosti a počiatočnej rýchlosti (v-v0, čiže Δv). Jeho obsah teda bude 1/2•Δv•t. Za Δv si môžeme dosadiť vzorec na jeho výpočet, čiže a•t. Vyjde nám teda vzorec 1/2•a•t•t, čiže 1/2•a•t2. Tieto obsahy spočítame, a tak vyjde nám vzorec s=v0•t+1/2•a•t2 respektíve s=v0•t+1/2•a•Δv•t.
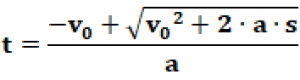 Pomocou klasických ekvivalentných úprav rovnice si vieme odvodiť vzorec na výpočet počiatočnej rýchlosti (v0=s/t -1/2•a•t, resp. v0= - 2s/t - v) a rýchlosti (v=2•s/t - v0). Vzorec pre čas sa odvodzuje ťažšie, keďže ide o kvadratickú rovnicu (t.j. vzorec na výpočet dráhy obsahuje druhú mocninu). Vzorec pre čas je zobrazený na obrázku vpravo hore. Ak používame tento vzorec na počítanie s rovnomerne spomaleným pohybom (pozri nižšie), môže nastať aj prípad, že výraz nebude mať riešenie, keďže pod odmocninou bude vychádzať záporné číslo. V takom prípade to znamená, že teleso danú dráhu nikdy neprejde, pretože zastane (zníži rýchlosť na nulu) ešte predtým, ako by ju prešlo.
Pomocou klasických ekvivalentných úprav rovnice si vieme odvodiť vzorec na výpočet počiatočnej rýchlosti (v0=s/t -1/2•a•t, resp. v0= - 2s/t - v) a rýchlosti (v=2•s/t - v0). Vzorec pre čas sa odvodzuje ťažšie, keďže ide o kvadratickú rovnicu (t.j. vzorec na výpočet dráhy obsahuje druhú mocninu). Vzorec pre čas je zobrazený na obrázku vpravo hore. Ak používame tento vzorec na počítanie s rovnomerne spomaleným pohybom (pozri nižšie), môže nastať aj prípad, že výraz nebude mať riešenie, keďže pod odmocninou bude vychádzať záporné číslo. V takom prípade to znamená, že teleso danú dráhu nikdy neprejde, pretože zastane (zníži rýchlosť na nulu) ešte predtým, ako by ju prešlo.
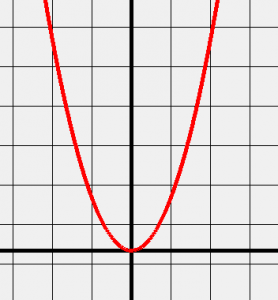
Keď si nakreslíme graf závislosti dráhy od času pri pohybe s konštantným zrýchlením, tak vidíme takú krivku, aká je zobrazená na obrázku nižšie vpravo. Je to časťou krivky, ktorá sa volá parabola (tá je zobrazená na obrázku nižšie vľavo).
 |
 |
| Takto vyzerá parabola. | Takto vyzerá graf rovnomerne zrýchleného pohybu - pravá časť paraboly. |
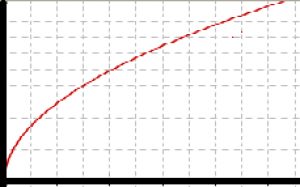 Špeciálnym druhom pohybu s konštantným zrýchlením je rovnomerne spomalený pohyb. Počíta sa s ním rovnako ako s bežným rovnomerne zrýchleným pohybom, akurát že zrýchlenie je záporné. Priamka, ktorá tvorí graf závislosti rýchlosti od času, je klesajúca. Graf závislosti dráhy od času je stále parabola, avšak inak otočená (pozri obrázok vľavo).
Špeciálnym druhom pohybu s konštantným zrýchlením je rovnomerne spomalený pohyb. Počíta sa s ním rovnako ako s bežným rovnomerne zrýchleným pohybom, akurát že zrýchlenie je záporné. Priamka, ktorá tvorí graf závislosti rýchlosti od času, je klesajúca. Graf závislosti dráhy od času je stále parabola, avšak inak otočená (pozri obrázok vľavo).
Aj voľný pád je rovnomerne zrýchlený pohyb. Ako zrýchlenie do vzorca uvádzame tiažové zrýchlenie (g), ktoré má v našej zemepisnej šírke hodnotu 9,81m•s-2, na rovníku 9,78m•s-2 a na póloch 9,83m•s-2. Tiažové zrýchlenie je ovplyvnené okrem geografickej polohy aj nadmorskou výškou, to však takmer vždy môžeme zanedbať. Často používame aj zaokrúhlenú hodnotu 10m•s-2. Voľný pád je rovnaký pre všetky telesá (čiže voľným pádom bude pierko padať rovnako ako kameň). Ale na našu planétu nemožno spadnúť voľným pádom, keďže má atmosféru, a teda bude brzdené odporom vzduchu. Ten však môžeme zanedbať, pokiaľ je padajúce teleso malé a súčasne ťažké (napríklad kamene atď.), a tak pád považovať za voľný.
3 Newtonove pohybové zákony
1. Newtonov pohybový zákon (zákon zotrvačnosti): teleso zotrváva vo svojom pohybovom stave (pokoji alebo rovnomernom pohybe), pokiaľ naň nepôsobý žiadna vonkajšia sila, alebo pokiaľ sú sily, ktoré naň pôsobia, v rovnováhe. Tento zákon vysvetľuje, prečo nás hodí dopredu, keď sedíme v autobuse a autobus zabrzdí. Zákon zotrvačnosti využívame napríklad pri prášení kobercov (prakerom koberec uvedieme do pohybu, potom zastavíme a čiastočky prachu odletia preč. Ďalšie jeho zaujímavé využitie je zisťovanie, či je vajíčko surové alebo uvarené. Vajíčko roztočíme, zastavíme a pustíme. S uvareným sa nič nestane, ale surové sa začne znovu hýbať, lebo jeho vnútro je tekuté, a teda sa môže voľne pohybovať a zotrvačnosťou z točenia vajíčko znovu rozhýbe.
2. Newtonov pohybový zákon (zákon sily): zrýchlenie telesa je priamoúmerné vynaloženej sile a nepriamoúmerné jeho hmotnosti. Čiže zrýchlenie vieme vyjadriť ako a=F/m. Keď si z tohto vzorca vyjadríme silu, dostaneme vzorec F=m•a. Dosaďme si do tohto vzorca jednotky a čo nám vyjde? Jednotka sily newton vyjadrená pomocou kombinácie základných jednotiek (N=kg•m•s-2).
3. Newtonov pohybový zákon (zákon akcie a reakcie): každá akcia vyvoláva reakciu rovnakej veľkosti ale opačného smeru. Akcia a reakcia sa navzájom nerušia, lebo každá z nich pôsobí na iné teleso. Keď teda kopnem do lopty, pôsobím na ňu silou, ale lopta pôsobí rovnakou silou na mňa. Akurát že ja som ťažší, čiže na moje rozhýbanie by bola potrebná (v zmysle 2. Newtonovho zákona) väčšia sila. Zákon akcie a reakcie vysvetľuje napríklad, prečo majú strelné zbrane spätný úder (spätný náraz). Tento zákon využívame napríklad v raketových motoroch (pri spaľovaní paliva vznikne veľa horúcich plynov, ktoré v rakete nemajú miesto, a preto unikajú von veľkou rýchlosťou; rovnakou silou ako sú plyny z rakety vytláčané, je raketa tlačená do opačného smeru). Preto sa tieto motory nazývajú aj reaktívne.
|
1.) Zadanie: Autíčko sa pohybuje 4 sekundy rovnomerným pohybom rýchlosťou 2m/s. Akú dráhu prejde? (Táto úloha je taká jednoduchá, že ani nepíšem zápis.) Výpočet: s=v•t=2m/s•4s=8m Odpoveď: Autíčko prejde dráhu 8m. |
|
2.) Zadanie: Cyklista prešiel dráhu 10km za 25 minút. Aká bola jeho priemerná rýchlosť? Vyjadrite to v kilometroch za hodinu aj v metroch za sekundu.
dráha cyklistu (s)....................................10km=10000m čas (t).....................................................25min=1500s≈0,41667h priemerná rýchlosť.................................?
Výpočet: v=s/t=10km/0,41667h≈24km/h≈6,7m/s
Odpoveď: Priemerná rýchlosť cyklistu bola 24km/h, čiže 6,7m/s. |