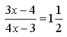Lineárne rovnice a slovné úlohy riešené pomocou nich

1. 1. 2017

Rovnica je rovnosť dvoch výrazov.

Koreň (riešenie) rovnice je číselná hodnota neznámej v rovnici. Zapisujeme ho ako K=číslo alebo K={číslo}.

Keď vyriešime rovnicu, môžeme urobiť skúšku správnosti. A to tak, že si vypočítame obe strany a overíme, či sa rovnajú. Ľavú stranu označujeme LS(left side) a pravú stranu RS(right side).

Ako riešiť rovnice

Ekvivalentné úpravy a základný princíp riešenia rovníc

Ekvivalentné úpravy sú úpravy, ktoré nezmenia riešenie rovnice. Zapisujeme ich tak, že za rovnicu zapíšeme lomenú čiaru a za ňu daný úkon. Ekvivalentné úpravy sú:

Výmena strán rovnice
Pripočítanie alebo odpočítanie toho istého čísla od oboch strán rovnice
Vynásobenie alebo vydelenie oboch strán rovnice tým istým nenulovým číslom
Náhrada výrazu na jednej, alebo na oboch stranách rovnice iným výrazom rovnakej hodnoty

Rovnicu riešime tak, že sa pomocou ekvivalentných úprav snažíme dostať všetky členy s premennou(neznámou) na jednu stranu a všetky členy bez premennej na druhú stranu.

Počet riešení lineárnej rovnice

Každá lineárna rovnica môže mať buď žiadne, jedno, alebo nekonečne veľa riešení.

Vo väčšine prípadov má lineárna rovnica jedno riešenie. Jedno riešenie má vtedy, ak nám vyjde premenná, ktorá sa rovná... Táto záverečná rovnosť je jediným riešením rovnice.

Ak nám vyjde niečo takéto (0x=0) resp. pravdivé tvrdenie (lebo 0x =0 si môžeme upraviť na 0=0), tak má rovnica nekonečne veľa riešení, lebo za x si môžem dosadiť akékoľvek číslo a stále nám vyjde 0. Ak má rovnica nekonečne veľa riešení, stačí skúšku správnosti urobiť pre jedno ľubovoľné číslo.

Ak nám vyjde niečo takéto (0x=5), resp. nepravdivé tvrdenie (lebo 0x=5 si môžem upraviť na 0=5), tak rovnica nemá riešenie, lebo žiadne číslo vynásobené nulou nám nedá 5 ani akékoľvek iné prirodzené číslo. Ak rovnica nemá riešenie, skúšku správnosti nerobíme.

Vyrieš rovnice

(správne riešenia a skúšky sú na konci príspevku)

a) 10x-1=15-6x

b) 1,2-^x/_1,2+4,5x-^x/_4,5=5,6+x

c) (2x-³/₂)x-1=(2x-1)(x-⁵/₂)

e) 2(3+4x)-2=3-5(1-x)

(viac rovníc aj s riešeniami nájdeš na priklady.com)

Rovnice s neznámou v menovateli

Pri riešení rovníc, ktoré obsahujú výrazy s neznámou v menovateli musíme určiť podmienku, kedy má lomený výraz (výraz s neznámou v menovateli) zmysel, čiže keď sa menovateľ zlomku nemôže rovnať nule. Napríklad výraz ¹/_2+x má zmysel, ak x≠-2, lebo 2+(-2)=0. Podmienku píšeme tak, že za ekvivalentnú úpravu napíšeme bodkočiarku a potom premennú a ≠.

**Vyrieš rovnice** a urči podmienku riešiteľnosti (správne riešenia sú na konci príspevku):
g)	h)
i)	j)
k)	l)

(viac rovníc aj s riešeniami nájdeš na priklady.com)

Slovné úlohy riešené pomocou rovníc

Slovné úlohy s dvomi rovnými tvrdeniami

Ako riešiť pomocou rovnice úlohy s dvomi tvrdeniami
Moja mama je odo mňa o 27 rokov staršia. O 10 rokov bude 2,08 krát staršia ako ja. Koľko rokov mám a koľko rokov má moja mama?
Najprv si urobíme zápis s údajmi o oboch tvrdeniach.	Môj vek teraz...................x Mamin vek teraz........x+27 Môj vek o 10 rokov....x+10 Mamin vek o 10 rokov...............2,08•(x+10)
Potom si zostavíme a vyriešime rovnicu. Musíme vychádzať z tvrdení, ktoré sa rovnajú. Keďže vek mojej mamy bude o 10 rokov 2,08-krát vyšší ako môj, tak sa x+10 (môj vek vyšší o 10 rokov) vynásobené 2,08 (2,08•(x+10)) bude rovnať maminmu veku (x+27) zvýšenému o desať rokov (x+27+10).	x+27+10=2,08•(x+10) x+37=2,08x+20,8 /-2,08x -1,08x+37=20,8 /-37 -1,08x=-16,2 /:(-1,08) x=15
Potom odpovieme na otázku.	Mám 15 rokov (keďže môj vek je x a v rovnici nám vyšlo že x=15) a mama má 42 rokov (keďže je odo mňa o 27 rokov staršia a 15+27=42).

Vyrieš slovné úlohy (správne riešenia sú na konci príspevku):

1.) Počas chrípkovej epidémie ochorelo v pondelok 10% žiakov školy v utorok ďalších 39 žiakov a v stredu ešte jedna osmina všetkých žiakov školy. Za tieto tri dni ochorela spolu tretina všetkých žiakov školy. Koľko žiakov má škola a koľko ich ochorelo?

2.) Firma kúpila 20 tabletov a 15 notebookov za celkovú sumu 6000€. Vypočítaj cenu jedného tabletu a notebooku, ak vieš, že tablet bol o 50€ lacnejší ako notebook.

3.) Priemerná výška šiestich kamarátov je 181cm. Prišiel medzi nich Rasťo, čím sa priemerná výška znížila o 2 cm. Vypočítaj Rasťovu výšku.

Slovné úlohy o zmesiach

Ako riešiť pomocou rovnice úlohy o zmesiach
Zmiešali sme 2 litre vody s teplotou 30°C s 3 litrami vody s teplotou 5°C. Akú teplotu má vody, ktorú sme tak dostali? Počítame s idealizovanými podmienkami, že žiadne teplo neunikne.
Najprv si urobíme zápis s množstvami vody a jej teplotami.	1.voda: 2l........................30°C 2.voda: 3l........................5°C Výsledná voda: 5l...........x°C
Pri zostavovaní rovnice vychádzame z fyzikálneho zákona, ktorý hovorí, že koľko tepla odovzdá jedna látka, toľko musí druhá prijať. Fyzikálny vzorec pre výpočet prijatého resp. odovzdaného tepla je Q(teplo)=m(hmotnosť)•c(hmotnostná tepelná kapacita)•Δt(zmena teploty). Keďže rátame s jednou látkou(vodou), hmotnostné tepelné kapacity na oboch stranách budú rovnaké, rovnaké, môžeme ich vynechať. Rovnaké budú aj hustoty, teda hmotnosť môžeme nahradiť objemom. Zmena teploty je vlastne rozdiel výslednej a pôvodnej teploty. Keďže nechceme, aby nám vyšlo záporné číslo a výsledná teplota je medzi vyššou a nižšou teplotou, tak od vyššej teploty budem výslednú teplotu odpočítavať a od výslednej teploty budem odpočítavať nižšiu teplotu.	Q₁=Q₂ m₁•c•(t₁-t₂)=m₂•c•(t₂-t₃) V₁•(t₁-x)=V₂•(x-t₂) 2•(30-x)=3•(x-5) (jednotky veličín nepíšem) 60-2x=3x-15 /-60-3x -5x=-75 /:(-5) x=15
Výsledok rovnice bude výsledná teplota.	Voda má 15°C.

Tento postup sa dá využiť aj pri príkladoch pri príkladoch o zmiešavaní roztokov s rôznym percentuálnym obsahom rozpustenej látky, s rôznou cenou atď... Vždy pri podobnú rovnicu ako vo vyššie uvedenom príklade: množstvo látky s väčšou hodnotou•(jej hodnota - výsledná hodnota)=množstvo látky s menšou hodnotou•(výsledná hodnota - jej hodnota).

Vyrieš slovné úlohy (správne riešenia sú na konci príspevku):

4.) V lekárni pridali k 3 litrom 95-percentného liehu 5 litrov 38,04-percentného liehu. Koľkopercentný lieh dostali?

5.) V obchode so sypanými čajmi predávajú jeden druh čaju po 24€/kg a druhý druh po 56€/kg. Ich zmes v pomere 5:3 pomáha liečiť ochorenia dýchacích ciest. Aká bude cena za kilogram tejto zmesi ak za namiešanie si predajca účtuje 20% z cien samotných surovín?

6.) Do 3dcl vody s teplotou 20°C som primiešal 5dcl vody. Aká bola jej teplota, ak teplota výslednej zmesi je 25°C?

Slovné úlohy o spoločnej práci

Ako riešiť pomocou rovnice úlohy o spoločnej práci
Môj otec pokosí záhradu za 2 hodiny. Ja pokosím záhradu za 3 hodiny. Koľko nám to bude trvať spolu?
Najprv si urobíme zápis, v ktorom zohľadníme koľko práce vykonajú jednotliví vykonávatelia za jednu hodinu a za x hodín.	Celá za 1h za xh Ja...........za 3h...........¹/₃................^x/₃ Otec.......za 2h...........¹/₂................^x/₂
Potom zostavíme rovnicu, v ktorej bude na jednej strane súčet prác, ktoré vykonajú vykonávatelia za x hodín a na druhej strane množstvo práce, ktorú musia vykonať (v tomto prípade musíme pokosiť jednu záhradu)	^x/₃+^x/₂=1 /•2•3 (•6) 2x+3x=6 5x=6 /:5 x=1,2
X sa rovná času, za ktorý vykonávatelia prácu spolu vykonajú.	1,2h=1h12min Spolu nám to bude trvať hodinu a dvanásť minút.

Vyrieš slovné úlohy (správne riešenia sú na konci príspevku):

7.) Gazda od šiestej rána kosí lúku. Bude mu to trvať 12 hodín. Keďže na poobedie hlásili búrky, prišli mu po hodine na pomoc jeho dvaja synovia a všetci to zvládli do do desiatej. Za aký dlhý čas by pokosili lúku synovia?

8.) Prvým prítokom sa naplní celá vaňa za 12min, druhým za 15 min do troch štvrtín. Ako dlho by trvalo naplnenie vane do polovice obomi prítokmi naraz?

9.) Otec by sám obral jablká za 8 dní. Po dvoch začal oberať aj syn a poďalších štyroch dňoch oberačku skončili. Za koľko dní by obral jablká syn sám?

Slovné úlohy o pohybe

Ako riešiť úlohy o pohybe za sebou
1.auto vyrazilo s priemernou rýchlosťou 70km/h. O polhodinu z toho istého miesta vyrazilo 2.auto s priemernou rýchlosťou 90km/h. Ako dlho bude trvať druhému autu, kým dobehne prvé? (Predpokladáme, že autá nikde nezastanú a priemerná rýchlosť sa nezmení.)
Najprv si urobíme náčrt.	v₁=70 km/h v₂=90km/h t₁=xh t₂=xh-0,5h s₁=70•x s₂=90•(x-0,5)
Urobíme si zápis. Rýchlosti poznáme. Čas prvého auta si označíme x. Keďže druhé auto vyráža o polhodinu neskôr, tak jeho čas bude o polhodinu kratší (xh-0,5h). Pri zápise dráhy využijeme fyzikálny vzorec, ktorý hovorí, že s=v•t (dráha sa rovná rýchlosť krát čas). A teda oba časy vynásobíme rýchlosťami.
Ani rýchlosi, ani časy nie sú rovnaké. Ale z obrázku vidíme, že rovnaké sú dráhy. A teda výpočet dráh oboch áut zo zápisu dosadíme do rovnice, ktorú vyriešime. Keďže ako x sme si označili čas prvého auta, a my chceme čas druhého auta, tak si od koreňa ešte odpočítame 0,5h.	s₁=s₂ 70x=90(x-0,5) (jednotky nepíšem) 70x=90x-45 /-90x -20x=-45 /:-20 x=2,25 2,25-0,5=1,75
Napíšeme odpoveď.	Druhému auto to bude trvať 1,75h, čiže 1h45min.

Ako riešiť úlohy o pohybe oproti sebe
Fero išiel na návštevu k Paľovi do susednej dediny vzdialenej 15 kilometrov. Vyrazil o 10:00 bicyklom priemernou rýchlosťou 20 km/h. Po desiatich minútach sa mu Paľo vybral oproti bicyklom priemernou rýchlosťou 25 km/h. Kedy a v akej vzdialenosti od Ferovej dediny sa stretnú?
Najprv si urobíme náčrt.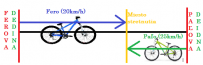
Potom si urobíme zápis. Rýchlosti poznáme. Ferovu dráhu označíme x, tak Paľova dráha bude rozdiel celkovej dráhy (čiže 15 km) a Ferovej dráhy. Na vyjadrenie časov využijeme fyzikálny vzorec: t=^s/_v (čas sa rovná dráhe vydelenej rýchlosťou).	s₁=x km s₂=15-x km v₁=20 km/h v₂=25 km/h t₁=^x/₂₀ t₂=^15-x/₂₅
Teraz nie je rovnaká ani dráha, ani rýchlosť, ani čas. Ale pri zostavení rovnice môžeme využiť fakt, že Paľov čas je kratší o 10 minút, čiže k Paľovej strane ich musíme pripočítať, aby sme dosiahli rovnosť. Keďže rýchlosti sú uvedené v km/h, tak aj čas musí byť v hodinách. 10min si teda premeníme na ¹/₆h.	t₁=t₂+¹/₆ (jednotky nepíšem) ^x/₂₀=^15-x/₂₅+¹/₆ /•300 (najmenší spoločný násobok) 15x=12(15-x)+50 15x=180-12x+50 /+12x 27x=230 /:27 x=²³⁰/₂₇=8¹⁴/₂₇≈8,519 t≈8,519km:20km/h=0,42595h≈26min
Vzdialenosť od Ferovej dediny je x. Keď x vydelíme Ferovou rýchlosťou, dostaneme čas, ktorý bude trvať Ferovi aby sa dostal na miesto stretnutia. Pripočítajme ho k času, kedy vyštartoval, a máme čas stretnutia.	Fero a Paľo sa stretnú o 10:26 a 8,519km od Ferovej dediny.

Vyrieš slovné úlohy (správne riešenia sú na konci príspevku):

10.) Kamión vyrazil priemernou rýchlosťou 54km/h a o 2 hodiny neskôr za ním vyrazilo auto, ktoré ho dobehlo o 3,5h. Akou priemernou rýchlosťou išlo auto?

11.) Medzi letiskami vzdialenými 1840km od seba lietajú pravidelné spoje. Z prvého štartuje lietadlo o 7:00, z druhého o 8:00. Prvé letí priemernou rýchlosťou o 50km/h vyššou ako druhé. V akej vzdialenosti od prvého letiska sa stretávajú vždy o 9:00?

12.) Od Fera k Janovi je to 12km. Ráno o 7:00 vyrazili obaja obaja oproti sebe po tej istej ceste. Fero išiel priemernou rýchlosťou 5km/h, Jano o 2km/h pomalšie. Ako ďaleko od Ferovho domu sa stretli a koľko bolo hodín?

Vyjadrenie neznámej zo vzorca

Vzorec pre teplo(Q) je Q=m•c•Δt. Aký bude vzorec pre zmenu teploty(Δt)? Aj vzorce sú vlastne rovnice, a to sa dá využiť pri ich odvodzovaní:

m•c•Δt=Q /:m

c•Δt=^Q/_m /:c

Δt=^Q/_m•c

Ale čo ak máme nejaký takýto vzorec: S=a•b+a•c+b•c ? Tu máme problém, keďže dva členy majú jednu rovnakú a jednu rôznu premennú. Ale tu si pomôžeme vynímaním pred zátvorku. Vyjadrime si teda a:

a•b+a•c+b•c =S /-b•c

a•b+a•c=S-b•c

a•(b+c)=S-b•c /:(b+c)

a=^S-b•c/_b+c

Niečo navyše

Vytvor si rovnicu pre x=...

Ak chceme vytvoriť rovnicu pre x=..., tak si najprv napíšeme danú rovnosť a potom ju pomocou ekvivalentných úprav robíme zložitejšou.

Napríklad:

x=7 /•3

3x=21 /+4x

7x=21+4x /•5

35x=5(21+4x) /-2x-4

33x-4=5(21+4x)-2x-4 atď. atď.

Premena periodických desatinných čísel na zlomky pomocou rovníc

Každý zlomok vieme premeniť na desatinné číslo. To desatinné číslo môže mať buď ukončený desatinný rozvoj (napr. ¹/₄=0,25) alebo opakujúci sa (periodický) desatinný rozvoj (napr. ¹/₃=0,33333...). Perióda je donekonečna sa opakujúca časť v periodickom desatinnom čísle. Rýdzo periodické číslo je číslo, ktoré má v perióde len 1 číslicu. Nerýdzo periodické číslo je periodické číslo, ktoré má v perióde 2 a viac číslic. Rovnako ako každý zlomok má prislúchajúce desatinné číslo, tak každé desatinné číslo s ukončeným alebo opakujúcim sa desatinným rozvojom má prislúchajúci zlomok. Ale ako periodické číslo premeniť na zlomok?

Premena jednoduchých periodických čísel na zlomky
Ak sa celá časť periodického čísla rovná nule a perióda nasleduje hneď po desatinnej čiarke, môžeme použiť tento postup: 1. Napíšeme si rovnicu, ktorej ľavá strana bude x a pravá strana dané číslo. 2. Rovnicu vynásobíme takou mocninou desiatky (10, 100, 1000 atď.), aby sa celá časť daného periodického čísla rovnala číslu vo vnútri periódy.
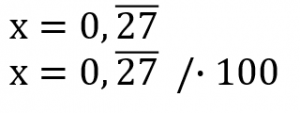3. Od rovnice odpočítame periódu. Keďže pôvodná rovnica ukazuje, že perióda sa vlastne rovná x, od ľavej strany iba odpočítame x.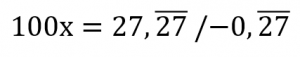
4. Rovnicu vydelením upravíme tak, že na ľavej strane bude iba x. Pravú stranu delením upravíme na zlomok.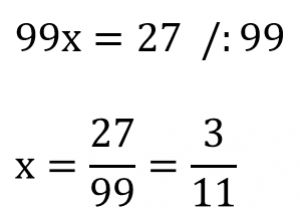

Periodické čísla, ktoré majú celú časť inú ako 0 alebo ich perióda nenasleduje hneď za desatinnou čiarkou, musíme najprv rozložiť na desatinné čísla s ukončeným desatinným rozvojom a periodické číslo spĺňajúce vyššie uvedené podmienky. Čiže číslo 3,45363636... premeníme na zlomok takto:

Riešenia

Riešenia rovníc a-f
a) 10x-1=15-6x /+6x 16x-1=15 /+1 16x=16 /:16 x=1 K=1 Skúška správnosti: LS=10•1-1=9 RS=15-6•1=9 LS=RS	b) 1,2-^x/_1,2+4,5x-^x/_4,5=5,6+x /•1,2 1,44-x+5,4x-¹^,2x/_4,5=6,72+1,2x 1,44+4,4x-^1,2x/_4,5=6,72+1,2x /•4,5 6,48+19,8x-1,2x=30,24+5,4x 6,48+18,6x=30,24+5,4x /-5,4x 6,48+13,2x=30,24 /-6,48 13,2x=23,76 /:13,2 x=1,8 K=1,8 Skúška správnosti: LS=1,2-^1,8/_1,2+4,5•1,8-^1,8/_4,5= =1,2-1,5+8,1-0,4=7,4 RS=5,6+1,8=7,4 LS=RS
c) (2x-³/₂)x-1=(2x-1)(x-⁵/₂) 2x²-³/₂x-1=2x²-5x-x+⁵/₂ /-2x² -³/₂x-1=-6x+⁵/₂ /+6x=+¹²/_2x ⁹/₂x-1=⁵/₂ /+1=+²/₂ ⁹/₂x=⁷/₂ /:⁹/₂=•²/₉ x=⁷/₉ K=⁷/₉ Skúška správnosti: LS=(2•⁷/₉-³/₂)•⁷/₉-1=(¹⁴/₉-³/₂)•⁷/₉-1= =(²⁸/₁₈-²⁷/₁₈)•⁷/₉-1=¹/₁₈•⁷/₉-1= =⁷/₁₆₂-¹⁶²/₁₆₂=-¹⁵⁵/₁₆₂ RS=(2•⁷/₉-1)(⁷/9-⁵/₂)= =(¹⁴/₉-⁹/₉)(¹⁴/₁₈-⁴⁵/₁₈)=⁵/₉•(-³¹/₁₈)= =-¹⁵⁵/₁₆₈ _LS=RS	d)
e) 2(3+4x)-2=3-5(1-x) 6+8x-2=3-5+5x /-5x 4+3x=-2 /-4 3x=-6 /:3 x=-2 Skúška správnosti: LS=2(3+4•(-2))-2=2•(-5)-2=-12 RS=3-5(1-(-2))=3-5•3=-12 LS=RS	f)

Späť k rovniciam

Riešenia rovníc s neznámou v menovateli (g-l)
g) /•(x+1)•2x; x≠-1 x≠0 2x=x+1 /-x x=1 Skúška správnosti: LS=¹/₁₊₁=0,5 PS=¹/_2•1=0,5 LS=RS	h) /•(x-3)•(x-2)•(x-4); x≠3 x≠2 x≠4 4(x-2)(x-4)-3(x-3)(x-4)=(x-3)(x-2) 4x²-16x-8x+32-3x²+12x+9x-36= =x²-2x-3x+6 x²-3x-4=x²-5x+6 /-x²+5x+4 2x=10 /:2 x=5 Skúška správnosti: LS=⁴/_5-3-³/_5-2=2-1=1 RS=¹/_5-4=1 LS=RS
i) /•(x-8); x≠8 x-4=5(x-8) x-4=5x-40 /-5x+4 -4x=-36 /:(-4) x=9 Skúška správnosti: LS=^9-4/_9-8=5 RS=5 LS=RS	j) /•5x•10x²; x≠0 10x²(1-x)=5x(1-x)-0,2•5x•10x² 10x²-10x³=5x-5x²-10x³ /+10x³+5x² 15x²=5x /:5x 3x=1 /:3 x=¹/₃ Skúška správnosti: LS=RS
k) /•(4x-3); x≠³/₄ 3x-4=³/₂•(4x-3) 3x-4=6x-4,5 /-6x+4 -3x=-0,5 /:(-3) x=¹/₆ Skúška správnosti: RS=1¹/₂ LS=RS	l) /•5x•x; x≠0 x(2x-4)=2•5x 2x²-4x=10x /+4x 2x²=14x /:2x x=7 Skúška správnosti: RS=²/₇ LS=RS

Späť k rovniciam

Riešenia slovných úloh s dvomi tvrdeniami (1-3)
1.) Zadanie: Počas chrípkovej epidémie ochorelo v pondelok 10% žiakov školy v utorok ďalších 39 žiakov a v stredu ešte jedna osmina všetkých žiakov školy. Za tieto tri dni ochorela spolu tretina všetkých žiakov školy. Koľko žiakov má škola a koľko ich ochorelo? Zápis: všetci žiaci školy......................x pondelok.................................10%•x=0,1x utorok......................................39 streda......................................¹/₈x=0,125x spolu........................................¹/₃x Výpočet: 0,1x+39+¹/₈x=¹/₃x /•3•8=•24 2,4x+936+3x=8x 5,4x+936=8x /-8x-936 -2,6x=-936 /:(-2,6) x=360 ¹/₃•360=120 Odpoveď: Škola má 360 žiakov a za tieto tri dni ich spolu ochorelo 120.
2.) Zadanie: Firma kúpila 20 tabletov a 15 notebookov za celkovú sumu 6000€. Vypočítaj cenu jedného tabletu a notebooku, ak vieš, že tablet bol o 50€ lacnejší ako notebook. Zápis: cena notebooku..............................x cena tabletu....................................x-50 počet notebookov...........................15 počet tabletov.................................20 celková suma.................................6000 Výpočet: 15x+20(x-50)=6000 15x+20x-1000=6000 /+1000 35x=7000 /:35 x=200 200-50=150 Odpoveď: Notebook stál 200 eur a tablet stál 150 eur.
3.) Zadanie: Priemerná výška šiestich kamarátov je 181cm. Prišiel medzi nich Rasťo, čím sa priemerná výška znížila o 2 cm. Vypočítaj Rasťovu výšku. Zápis: prvotný počet..................................................6 prvotný priemer...............................................181 prvotný súčet..................................................181•6=1086 konečný počet.................................................7 Rasťova výška.................................................x konečný súčet.................................................1086+x konečný priemer..............................................179 Výpočet: ^1086+x/₇=179 /•7 1086+x=1253 /-1086 x=167 Odpoveď: Rasťova výška je 167cm.

Späť k úlohám

Riešenia slovných úloh o zmesiach (4-6)
4.) Zadanie: V lekárni pridali k 3 litrom 95-percentného liehu 5 litrov 38,04-percentného liehu. Koľkopercentný lieh dostali? Zápis: množstvo prvého liehu........................................3l koncentrácia prvého liehu..................................95% množstvo druhého liehu.....................................5l koncentrácia druhého liehu................................38,04% výsledné množstvo.............................................8l výsledná koncentrácia........................................x % Výpočet: 3(95-x)=5(x-38,04) 285-3x=5x-190,2 /-5x-285 -8x=-475,2 /:(-8) x=59,4 Odpoveď: Dostali 59,4-percentný lieh.
5.) Zadanie: V obchode so sypanými čajmi predávajú jeden druh čaju po 24€/kg a druhý druh po 56€/kg. Ich zmes v pomere 5:3 pomáha liečiť ochorenia dýchacích ciest. Aká bude cena za kilogram tejto zmesi ak za namiešanie si predajca účtuje 20% z cien samotných surovín? Zápis: cena prvého čaju..................................................24 €/kg cena druhého čaju................................................56 €/kg výsledné množstvo (rozdelené v pomere 3:5).....1kg množstvo prvého čaju..........................................0,625 kg množstvo druhého čaju........................................0,375 kg výsledná cena.......................................................x+0,2x Výpočet: 0,625(x-24)=0,375(56-x) 0,625x-15=21-0,375x /+0,375x+15 x=36 36•1,2=43,2 Odpoveď: Kilogram čajovej zmesi bude stáť 43,2€.
6.) Zadanie: Do 3dcl vody s teplotou 20°C som primiešal 5dcl vody. Aká bola jej teplota, ak teplota výslednej zmesi je 25°C? Zápis: množstvo prvej vody.............................................3dcl teplota prvej vody..................................................20°C množstvo druhej vody...........................................5dcl teplota druhej vody................................................x °C výsledná teplota....................................................25°C Výpočet: 3(25-20)=5(x-25) 15=5x-125 /-15-5x -5x=-140 /:(-5) x=28 Odpoveď: Jej teplota bola 28°C.

Späť k úlohám

Riešenia slovných úloh o spoločnej práci (7-9)
7.) Zadanie: Gazda od šiestej rána kosí lúku. Bude mu to trvať 12 hodín. Keďže na poobedie hlásili búrky, prišli mu po hodine na pomoc jeho dvaja synovia a všetci to zvládli do do desiatej. Za aký dlhý čas by pokosili lúku synovia? Zápis: celá lúka za 1h za 4h za 3h gazda...................za 12h................. ¹/₁₂...........⁴/₁₂=¹/₃.........³/₁₂=¹/₄ synovia.................za x h....................¹/_x.................⁴/_x.................³/_x Výpočet: ¹/₃+³/_x=1 /•3x; x≠0 x+9=3x /-3x-9 -2x=-9 /:(-2) x=4,5 Odpoveď: Synovia by lúku pokosili za 4,5h, čiže za 4h 30min.
8.) Zadanie: Prvým prítokom sa naplní celá vaňa za 12min, druhým za 15 min do troch štvrtín. Ako dlho by trvalo naplnenie vane do polovice obomi prítokmi naraz? Zápis: celá ³/₄ za 1 min za x min 1. prítok.......za 12 min........... - ......................¹/₁₂..............................^x/₁₂ 2. prítok...............-...............za 15 min............¹/₁₅•³/₄=¹/₂₀..................^x/₁₅•³/₄=^x/₂₀ Výpočet: ^x/₁₂+^x/₂₀=¹/₂ /•12•20=•240 20x+12x=120 32x=120 /:32 x=3,75 Odpoveď: Obomi prítokmi naraz sa vaňa naplní do polovice za 3,75min, čiže za 3min 45s.
9.) Zadanie: Otec by sám obral jablká za 8 dní. Po dvoch začal oberať aj syn a poďalších štyroch dňoch oberačku skončili. Za koľko dní by obral jablká syn sám? Zápis: všetky jablká za 6 (2+4) dní za 4 dni otec..................za 8 dní.......................⁶/₈=³/₄...............................⁴/₈=¹/₂ syn...................za x dní...........................⁶/_x......................................⁴/_x Výpočet: ³/₄+⁴/_x=1 /•4x 3x+16=4x /-4x-16 -x=-16 /•(-1) x=16 Odpoveď: Syn sám by jablká obral za 16 dní.

Späť k úlohám

Riešenia slovných úloh o pohybe (10-12)
10.) Zadanie: Kamión vyrazil priemernou rýchlosťou 54km/h a o 2 hodiny neskôr za ním vyrazilo auto, ktoré ho dobehlo o 3,5h. Akou priemernou rýchlosťou išlo auto? Zápis: v₁=54 km/h v₂=x km/h t₁=2h+3,5h=5,5h t₂=3,5h s₁=54 km/h • 5,5h=297km s₂=3,5x Výpočet: s₁=s₂ 3,5x=297 /:3,5 x≈85 km/h Odpoveď: Auto išlo priemernou rýchlosťou 85 km/h.
11.) Zadanie: Medzi letiskami vzdialenými 1840km od seba lietajú pravidelné spoje. Z prvého štartuje lietadlo o 7:00, z druhého o 8:00. Prvé letí priemernou rýchlosťou o 50km/h vyššou ako druhé. V akej vzdialenosti od prvého letiska sa stretávajú vždy o 9:00? Zápis: v₁=x km/h v₂=x km/h - 50 km/h t₁=2 h t₂=1 h s₁=2x s₂=x-50 Výpočet: s₁+s₂=1840 2x+x-50=1840 /+50 3x=1890 /:3 x=630 s₁=2•630=1260 Odpoveď: O 9:00 sa stretnú vo vzdialenosti 1260km od prvého letiska.
12.) Zadanie: Od Fera k Janovi je to 12km. Ráno o 7:00 vyrazili obaja obaja oproti sebe po tej istej ceste. Fero išiel priemernou rýchlosťou 5km/h, Jano o 2km/h pomalšie. Ako ďaleko od Ferovho domu sa stretli a koľko bolo hodín? Zápis: v₁=5 km/h v₂=5km/h-2km/h=3 km/h s₁=x km s₂=12 km - x km t₁=^x/₅ t₂=^12-x/₃ Výpočet: t₁=t₂ ^x/₅=^12-x/₃ /•3•5=•15 3x=5(12-x) 3x=60-5x /+5x 8x=60 /:8 x=7,5 Odpoveď: Stretnú sa vo vzdialenosti 7,5km od Ferovho domu.

Späť k úlohám

Rebelova škola doma

Menu

Lineárne rovnice a slovné úlohy riešené pomocou nich

Vyhľadávanie

Kontakt

Obľúbené odkazy