Rebelova škola doma

Geometrická optika je časť optiky, ktorá sa zaoberá odrazom a lomom svetla. Charakter týchto javov možno vysvetliť na základe tzv. Fermatovho princípu najmenšieho času, ktorý hovorí, že zo všetkých možných dráh, ktorými sa dá dostať z jedného bodu do druhého si svetlo vyberá takú, ktorú prejde za najkratší čas. Tento princíp okrem iného vysvetľuje aj to, prečo sa svetlo šíri priamočiaro (lebo priamka je najkratšia cesta z jedného bodu do druhého). Ako sa Fermatov princíp uplatňuje pri odraze a lome svetla, vysvetlím neskôr.

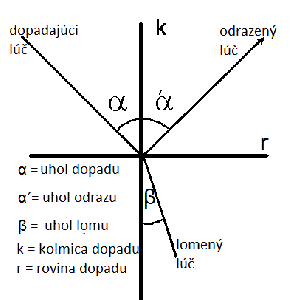Najprv si ujasníme pojmy rovina dopadu, kolmica dopadu, uhol dopadu, uhol odrazu a uhol lomu. Rovina dopadu je optické rozhranie, na ktoré svetlo dopadá. Kolmica dopadu je pomocná priamka, ktorá prechádza cez bod, v ktorom lúč dopadá na optické rozhranie. V prípade rovinného optického rozhrania je kolmá na rovinu dopadu a v prípade optického rozhrania tvaru časti kružnice alebo časti dutej gule smeruje do stredu danej kružnice alebo gule. Uhol dopadu (α) je uhol, ktorý zviera dopadajúci lúč s kolmicou dopadu. Uhol odrazu (α´) je uhol, ktorý zviera odrazený lúč s kolmicou dopadu. A uhol lomu (β) je uhol, ktorý zviera lomený lúč s kolmicou dopadu.

Budeme zobrazovať predmety v zrkadlách aj šošovkách. Obraz, ktorý vytvárajú, môže byť skutočný alebo neskutočný (zdanlivý). Skutočný obraz znamená, že na mieste jeho zobrazenia ho vieme zachytiť na tienidlo. Neskutočný (zdanlivý) obraz znamená, že na mieste jeho zobrazenia ho nevieme zachytiť na tienidlo, vidíme ho, iba keď sa pozrieme cez danú šošovku alebo do daného zrkadla (keď sa pozeráme do bežného zrkadla, zdá sa nám, akoby náš odraz stál niekde za zrkadlom, no v skutočnosti tam nikto nie je).

Odraz svetla

Zákon odrazu hovorí, že uhol dopadu sa rovná uhlu odrazu. Tento zákon vyplýva z Fermatovho princípu najmenšieho času.

Zrkadlo je teleso, ktoré má plochu, ktorá výborne odráža svetlo. Poznáme tieto druhy zrkadiel: rovinné (majú rovnú odrazovú plochu), duté (konkávne, majú odrazovú plochu tvaru vnútornej strany časti nejakej pravidelnej krivky, napríklad kružnice, dutej gule, elipsy, paraboly...), vypuklé (konvexné, majú odrazovú plochu tvaru vonkajšej strany nejakej pravidelnej krivky, napríklad kružnice, gule, elipsy, paraboly...) a krivé (ktorých odrazová plocha nemá pravidelný tvar). Rovinné zrkadlá sú bežné zrkadlá, aké máme doma na stene, duté zrkadlo je napríklad kozmetické zrkadielko, ktoré dáva zväčšený obraz a vypuklé zrkadlo je napríklad zrkadlo na križovatke, ktoré dáva zmenšený obraz.

Rovinné zrkadlo	Duté zrkadlo	Vypuklé zrkadlo

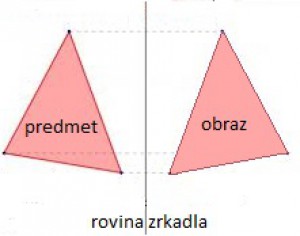Obraz predmetu v rovinnom zrkadle je rovnako veľký ako predmet, rovnako vzdialený od roviny zrkadla ako predmet, stranovo prevrátený a neskutočný (zdanlivý). Keď chceme zakresliť obraz predmetu v rovinnom zrkadle, všetky jeho body prenesieme súmerne na druhú stranu roviny zrkadla (čiže do rovnakej vzdialenosti od roviny zrkadla).

Niečo navyše: guľové zrkadlá

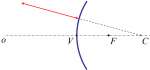
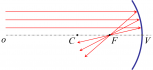
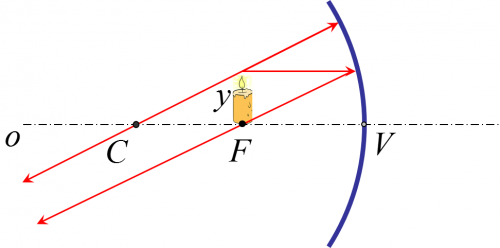
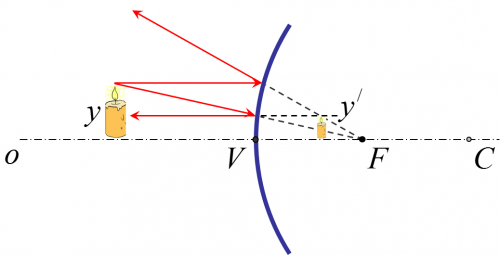
Guľové (sférické) zrkadlá sú zrkadlá, ktorých odrazovú plochu tvorí časť povrchu gule (guľový vrchlík). Pri dutom (konkávnom) guľovom zrkadle odráža svetlo vnútorná plocha gule a pri vypuklom (konvexnom) guľovom zrkadla odráža svetlo vonkajšia plocha gule. Rovnobežný svetelný zväzok sa po odraze na dutom zrkadle zmení na zbiehavý a po odraze na vypuklom zrkadle na rozbiehavý.

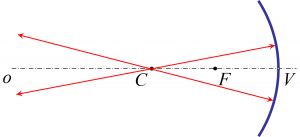
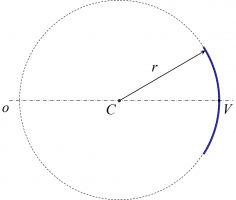
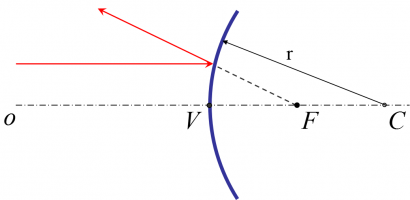
Stred krivosti zrkadla (C) je stred gule, ktorej vrchlík tvorí odrazovú plochu zrkadla. Pri dutom zrkadle leží pred zrkadlom a pri vypuklom zrkadle leží za zrkadlom.

Optická os zrkadla (o) je myslená priamka, ktorá je osou súernosti guľového vrchlíka, ktorý tvorí odrazovú plochu zrkadla. Prechádza stred krivosti. Vrchol zrkadla (V) je bod, v ktorom sa pretína optická os zrkadla s jeho odrazovou plochou. Jeho vzdialenosť od stredu krivosti zrkadla sa nazýva polomer krivosti zrkadla (r). Podľa dohody zvanej znamienková konvencia je polomer krivosti dutého guľového zrkadla kladný a polomer krivosti vypuklého guľevého zrkadla záporný.

Ohnisko (F) je bod, v ktorom sa pretínajú lúče pôvodne rovnobežného svetelného zväzku po odraze na guľovom zrkadle. Pri dutom zrkadle ho vidíme hneď a nazýva sa skutočné ohnisko. Pri vypuklom zrkadle je totožný s bodom, ktorý by bol zdrojom vzniknutého rozbiehavého svetelného zväzku a nazýva sa neskutočné ohnisko. Ohnisková vzdialenosť je vzdialenosť ohniska od vrcholu zrkadla. Dá sa dokázať, že ohniskoleží vždy v strede medzi stredom krivosti zrkadla a jeho vrcholom, a teda ohnisková vzdialenosť je polovica polomeru krivosti. Podľa znamienkovej konvencie je ohnisková vzdialenosť dutého guľového zrkadla kladná a ohnisková vzdialenosť vypuklého guľového zrkadla záporná.

Duté guľové zrkadlo	Vypuklé guľové zrkadlo

Aby sme zistili, ako sa nám v guľovom zrkadle zobrazí predmet, musíme si určiť (podobne ako pri šošovkách) tri tzv. význačné lúče (lúč prechádzajúci stredom krivosti, lúč rovnobežný s optickou osou a lúč prechádzajúci cez ohnisko).

1. Lúč, ktorý prechádza cez stred krivosti zrkadla, sa odráža v presne opačnom smere.
2. Lúč rovnobežný s optickou osou sa odráža do ohniska zrkadla.
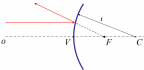
3. Lúč, ktorý prechádza cez ohnisko zrkadla sa odráža tak, aby bol rovnobežný s optickou osou.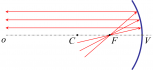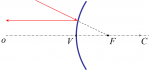

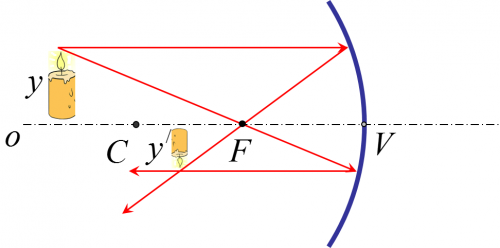
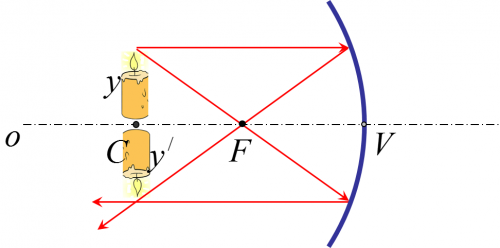
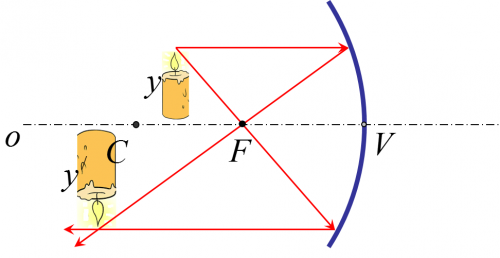
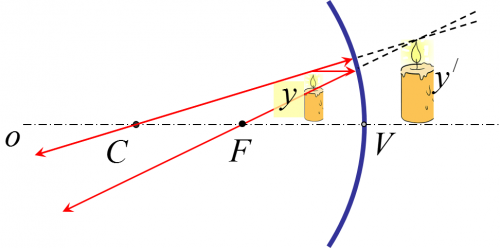
Pri zobrazovaní predmetu v dutom guľovom zrkadle môže natať v závislosti vzdialenosti predmetu od zrkadla 5 rôznych situácií. Pri zobrazovaní predmetu vo vypuklom guľovom zrkadle môže nastať len jedna možná situácia.

Zistiť, ako sa predmet zobrazí v guľovom zrkadle, však vieme nielen pomocou rysovania, ale aj pomocou výpočtu. Na tento výpočet využívame tzv. zobrazovaciu rovnicu guľového zrkadla: ¹/_a+¹/_a´=¹/_f=²/_r  (čiže súčet prevrátených hodnôt vzdialenosti predmetu a vzdialenosti obrazu od zrkadla sa rovná prevrátenej hodnote ohniskovej vzdialenosti, čiže prevrátenej hodnote polovice priemeru, čiže dvojnásobku prevrátenej hodnoty priemeru). Zobrazovacia rovnica však platí nielen pre vzdilaenosť predmetu a obrazu od zrkadla, ale aj pre výšku predmetu.

Avšak zákonitosti, ktoré sme si tu uviedli, platia len pre tzv. paraxiálne lúče, čiže pre lúče v blízkosti optickej osi. Tieto lúče sa nachádzajú v tzv. paraxiálnom priestore, čiže v prestore v blízkosti optickej osi. Osatné lúče sa nepretínajú presne v ohnisku. Čím má lúč väčšiu vzdialenosť od optickej osi, tým ďalej od ohniska je bod, v lúč naozaj pretína ostatné lúče. Preto obraz v guľovom zrkadle nie je celkom ostrý. Tento jav sa nazýva guľová chyba a odstránime ju tak, že namiesto guľového zrkadla použijeme parabolické zrkadlo, ktoré guľovú chybu nemá.

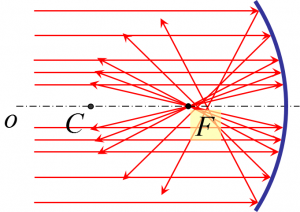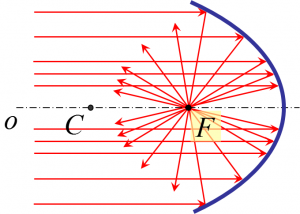Lúče odrazené v guľovom zrkalde	Lúče obdrazené v parabolickom zrkadle

Lom svetla

Už sme si povedali, že svetlo sa pri dopade na optické rozhranie láme. Príčinou tohto javu je skoková zmena rýchlosti. Aby sa zachoval Fermatov princíp najmenšieho času, svetlo sa láme tak, aby dlhšiu vzdialenosť prešlo v prostredí, v ktorom sa pohybuje rýchlejšie. Z toho vyplýva, že svetlo sa bude lámať smerom ku kolmici dopadu (β<α), ak prechádza z opticky redšieho prostredia do opticky hustejšieho prostredia (čiže jeho rýchlosť sa zmenší) a od kolmice dopadu (β>α), ak prechádza z opticky hustejšieho prostredia do opticky redšieho prostredia (čiže jeho rýchlosť sa zväčší). Veličina, ktorá vyjadruje to, ako sa svetlo bude lámať pri prechode z prostredia 1 do prostredia 2 sa volá relatívny index lomu (n_1,2).

Niečo navyše: výpočet uhla lomu pomocou relatívneho indexu lomu a výpočet relatívneho indexu lomu pomocou absolútnych indexov lomu

Ako z relatívneho indexu lomu vypočítať uhol lomu? Na to vám najprv musím predstaviť samotnú definíciu relatívneho indexu lomu. Relatívny index lomu sa rovná podielu sínusu uhla dopadu a sínusu uhla lomu (n_1,2=^sinα/_sinβ). Z tohto vzorca si vieme odvodiť že sínus uhla lomu vypočítame ako podiel sínusu uhla dopadu a relatívneho indexu lomu. Sínus uhla dopadu vieme vypočítať ako súčin sínusu uhla lomu a relatívneho indexu lomu.

Sú vo fyzikálnych tabuľkách uvedené indexy lomu na vštkých možných optických rozhraniach? Nie, lebo vypísať všetky kombinácie by zabralo zbytočne veľa miesta. Namiesto toho je tam pri každom jednom optickom prostredí uvedená hodnota inej veličiny, ktorá sa volá absolútny index lomu (n). Absolútny index lomu sa rovná relatívnemu indexu lomu pri prechode svetla z vákua do daného prostredia. Relatívny index lomu medzi prostrediami 1 a 2 vypočítame ako podiel absolútneho indexu lomu prostredia 2 a absolútneho indexu lomu prostredia 1 (n_1,2=^n₂/n₁).