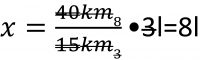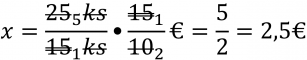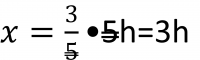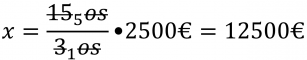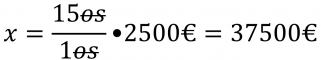Priama a nepriama úmernosť
Priama úmernosť je vzťah, v ktorom platí, že: v akom pomere sa zmení jedna veličina, v takom pomere sa zmení aj druhá veličina. Čiže: koľkokrát sa jedna veličina zväčší, toľkokrát sa zväčší aj druhá veličina. Koľkokrát sa jedna veličina zmenší, toľkokrát sa aj druhá veličina zmenší. Príklady: spotreba benzínu a prejdená vzdialenosť, cena a množstvo tovaru, čas a množstvo vykonanej práce.
Nepriama úmernosť je vzťah, v ktorom platí, že: v akom pomere sa zmení jedna veličina, v prevrátenom pomere sa zmení druhá veličina. Čiže: koľkokrát sa jedna veličina zväčší, toľkokrát sa druhá veličina zmenší. Koľkokrát sa jedna veličina zmenší, toľkokrát sa druhá veličina zväčší. Príklady: množstvo robotníkov a čas potrebný na vykonanie práce, rýchlosť a čas.
Trojčlenka: riešenie slovných úloh pomocou priamej a nepriamej úmernosti
Slovné úlohy, kde je priama a nepriama úmernosť, riešime pomocou trojčlenky:
| Potup riešenia | Riešenie aplikované na príklad |
|---|---|
|
1.Najprv si urobíme zápis skladajúci sa z dvoch stĺpcov, pričom každý z nich vyjadruje jednu veličinu. Neznámu označíme ako x. 2.Vedľa stĺpcov si umiestnime šípky. V prípade že ide o priamu úmernosť, šípky ukazujú rovnakým smerom, v prípade, že o nepriamu, navzájom opačným smerom. Od x ukazuje šípka vždy smerom nahor. |
Zápis: Toto je priama úmernosť, takže šípky budú ukazovať rovnakým smerom. ⇧15km......................3l⇧ ⇧40km......................xl⇧ |
|
3.Veličinu s obomi údajmi zapíšeme ako zlomok. Zlomok zapisujeme v smere šípky pri veličine. 4.Zlomok vynásobíme druhou veličinou. |
Výpočet:
|
|
5.Výsledok tohto násobenia je riešenie úlohy. |
Odpoveď: Na 40 kilometrov treba 8 litrov benzínu. |
|
Zadanie: 15 rožkov stojí 1,50€. Koľko stojí 25 rožkov?
Zápis:
Výpočet:
Odpoveď: 25 rožkov stojí 2€ a 50c. |
|
Zadanie: 3 robotníci urobia prácu za 2h. Ako dlho to bude trvať piatim robotníkom?
Zápis:
Výpočet:
Odpoveď: Piatim robotníkom to bude trvať 3 hodiny. |
|
Zadanie: Skupina 15 kamarátov si podala športku a vyhrali, pričom na každého pripadla výhra 2500€. Ak by ich bolo len 3, aká výhra by na jedného z nich pripadla? Aká bola celková výška výhry?
Zápis:
Výpočet:
Odpoveď: Ak by ich bolo len 3, na jedného z nich by pripadla výhra 12500€. Celková výška výhry bola 37500€. |
Úmernosti ako funkcie
Priama a nepriama úmernosť sú funkcie, a každá funkcia môže byť vyjadrená slovným zápisom, tabuľkou, rovnicou(vzorcom) a grafom.
Priama úmernosť ako funkcia
Na 15 kilometrov treba 3 litre benzínu. Koľko litrov benzínu treba na x km? (vzdialenosť si označíme ako veličinu x a objem benzínu ako veličinu y)
Najprv funkciu zadáme tabuľkou.
| x(km) | 1 | 2 | 3 | 5 | 10 | 15 |
|---|---|---|---|---|---|---|
| y(l) | 0,2 | 0,4 | 0,6 | 1 | 2 | 3 |
A teraz sa pokúsime odvodiť si rovnicu(vzorec): keď vytvárame trojčlenku, tvoríme zlomok ktorý násobíme druhou veličinou. Keďže však násobíme iba čitateľa, je úplne jedno, ktorá veličina bude v čitateli zlomku t.j. je úplne jedno či výpočet vyzerá takto(xl/15km•3km) alebo takto(3km/15km•xl). Teraz použime druhú verziu, aby sme si zlomok vyčíslili. Potom výpočet vyzerá takto: y=0,2•x. Toto je rovnica tejto priamej úmernosti. Nech si zoberieme akýkoľvek stĺpec v našej tabuľke a urobíme operáciu y:x, tak nám vyjde toto číslo(0,2). Je to teda konštanta. Každá priama úmernosť má takúto konštantu. Označme si ju písmenom k a v rovnici ním nahraďme číslo 0,2. Všeobecná rovnica priamej úmernosti teda je y=k•x.
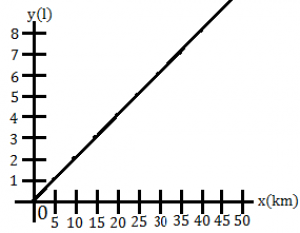
Ešte nám chýba graf. A tak si teda vytvoríme súradnicovú sústavu a do nej zakreslíme hodnoty z našej tabuľky. Os x zodpovedá veličine x a os y zodpovedá veličine y. Keď body zodpovedajúce hodnotám z tabuľky prepojíme, zistíme, že ležia na jednej priamke. Grafom priamej úmernosti je teda priamka alebo body ležiace na priamke. (Niekedy len body preto, lebo v niektorých prípadoch môžu vyjsť len celé čísla. Napríklad keď hovoríme o cene za kusy.)
Nepriama úmernosť ako funkcia
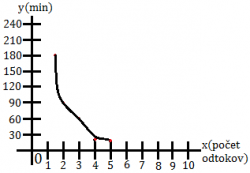
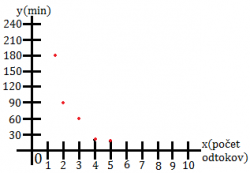
Dvomi odtokmi sa bazén vyprázdni za 1,5h(90min). Ako dlho to bude trvať x odtokom? (počet odtokov si označíme ako veličinu x a čas ako veličinu y).
Najprv funkciu zadáme tabuľkou:
| x(ks) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| y(min) | 180 | 90 | 60 | 45 | 36 | 30 |
A teraz sa pokúsime odvodiť si rovnicu(vzorec): keď vytvárame trojčlenku, tvoríme zlomok ktorý násobíme druhou veličinou. Keďže však násobíme iba čitateľa, je úplne jedno, ktorá veličina bude v čitateli zlomku t.j. je úplne jedno či výpočet vyzerá takto(90min/xks•2ks) alebo takto(90min•2ks/xks). Teraz použime druhú verziu, aby sme si čitateľa vyčíslili. Potom výpočet vyzerá takto: y=180/x. Toto je rovnica tejto nepriamej úmernosti. Nech si zoberieme akýkoľvek stĺpec v našej tabuľke a urobíme operáciu y•x, tak nám vyjde toto číslo(180). Je to teda konštanta. Každá nepriama úmernosť má takúto konštantu. Označme si ju písmenom k a v rovnici ním nahraďme číslo 180. Všeobecná rovnica priamej úmernosti teda je y=k/x.
Ešte nám chýba graf. A tak si teda vytvoríme súradnicovú sústavu a do nej zakreslíme hodnoty z našej tabuľky. Os x zodpovedá veličine x a os y zodpovedá veličine y. Teraz nemôžeme body prepojiť, lebo počet odtokov musí byť celé číslo. Ak by sme ich však prepojili, zistili by sme, že neležia na jednej priamke. Ležia na krivke, ktorá sa stále viac a viac približuje k osiam x aj y, no nikdy sa ich nedotkne. Takáto krivka sa nazýva hyperbola. Grafom nepriamej úmernosti je hyperbola alebo body ležiace na hyperbole.