Pravdepodobnosť a kombinatorika
Pravdepodobnosť
Pravdepodobnosť (hovorovo šanca, značka P) je číselné vyjadrenie istoty resp. neistoty nejakého javu. Hodnota pravdepodobnosti môže byť 0 až 1. Pravdepodobnosť istého javu je 1 a pravdepodobnosť nemožného javu je 0.
Pravdepodobnosť vypočítame tak, že počet priaznivých možností vydelíme počtom všetkých možností. Napríklad: Aká je pravdepodobnosť že keď hodím kocku, tak padne šestka? Šestka je na kocke jedna, čiže priaznivá možnosť je jedna. Všetkých čísel na kocke je 6, takže všetkých možností je 6. P=1/6.
Pravdepodobnosť môže byť vyjadrená zlomkom, pomerom, desatinným číslom alebo percentom. Pravdepodobnosť v predchádzajúcom príklade je vyjadrená zlomkom. Vyjadrená pomerom by vyzerala ako 1:6 desatinným číslom približne 0,1667, percentom približne 16,67%.
Ale ako počet možností vypočítať? Na to nám slúži kombinatorika.
Kombinatorika
Kombinatorika je odvetvie matematiky zaoberajúce sa študovaním počtom, výberom a usporiadaním objektov, ktoré vyhovujú zadaným kritériám. Čiže napríklad: Kritériá sú, že mám 4 hrnce a chcem vedieť, koľko je možností ich usporiadania. Pomocou kombinatoriky sa dá vypočítať, že ich je 24.
Riešenie vypísaním všetkých možností
Kombinatorické úlohy vždy vieme riešiť vypísaním všetkých možností. Hneď na začiatku však treba zvoliť systém, aby možnosti neboli usporiadané chaoticky a my aby sme tak vedeli, aké možnosti nám ešte ostávajú vypísať. Najjednoduchší systém je napísať si jedno ľubovoľné poradie a potom v ňom posltupne meniť najprv poslednú možnosť, potom predposlednú možnosť a poslednú možnosť atď.
| ABCD | BACD | CABD | DABC |
| ABDC | BADC | CADB | DACB |
| ACBD | BCAD | CBAD | DBAC |
| ACDB | BCDA | CBDA | DBCA |
| ADBC | BDAC | CDAB | DCAB |
| ADCB | BDCA | CDBA | DCBA |
Vidíme, že možností je 24.
| 111 | 211 | 311 |
| 112 | 212 | 312 |
| 113 | 213 | 313 |
| 121 | 221 | 321 |
| 122 | 222 | 322 |
| 123 | 223 | 323 |
| 131 | 231 | 331 |
| 132 | 232 | 332 |
| 133 | 233 | 333 |
Vidíme, že možností je 27.
Stromový diagram
Kombinatorické úlohy môžeme riešiť aj pomocou stromového diagramu. A to vtedy, ak máme istý počet možností a pre každú z nich istý počet možností a pre každú z nich istý počet možností atď. Stromový diagram tvoríme tak že zapíšeme prvotné možnosti a potom ku každej možnosti zapíšeme počet čiar, ktoré vyjadrujú počet druhotných možností prislúchajúcich danej prvotnej možnosti.
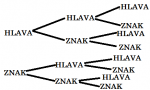 Mincu hádžem 3-krát. Koľko je možností usporiadania padnutí hlavy alebo znaku? Ak to chceme zo stromového diagramu zistiť, tak spočítame konečné možnosti. Vidíme, že ich je 8.
Mincu hádžem 3-krát. Koľko je možností usporiadania padnutí hlavy alebo znaku? Ak to chceme zo stromového diagramu zistiť, tak spočítame konečné možnosti. Vidíme, že ich je 8.
Riešenie pomocou tabuľky
| TÍM 1 | TÍM 2 | TÍM 3 | TÍM 4 | TÍM 5 | |
|---|---|---|---|---|---|
| TÍM 1 | ------- | ||||
| TÍM 2 | ------- | ||||
| TÍM 3 | ------- | ||||
| TÍM 4 | ------- | ||||
| TÍM 5 | ------- |
Vidíme, že možností je 20.
Permutácie, variácie, kombinácie a faktoriál
Permutácie bez opakovania vyjadrujú počet možností usporiadania daných objektov, ktoré však v jednej možnosti môžu byť len raz. Čiže napríklad vyššie uvedená úloha s možnosťami usporiadania písmen A, B, C, D.
Permutácie s opakovaním vyjadrujú počet možností usporiadania daných objektov, ktoré v jednej možnosti môžu byť ľubovoľne krát. Čiže napríklad vyššie uvedená úloha s usporiadaním číslic 1, 2, 3 alebo úloha s počtom možností hodu mince.
Variácie bez opakovania vyjadrujú počet možností výberu istého počtu objektov z istej množiny, pričom v jednom výbere môže byť jeden objekt maximálne raz a na poradí záleží (čiže A-B a B-A sú 2 rozdielne možnosti). Napríklad: Máme písmená A, B, C, D, E, F. Koľko máme možností výberu troch z nich ak záleží na poradí a v jednej možnosti môže byť každé písmeno maximálne raz? Možností bude 120.
Variácie s opakovaním vyjadrujú počet možností výberu istého počtu objektov z istej množiny, pričom v jednom výbere môže byť jeden objekt ľubovoľne krát a na poradí záleží (čiže A-B a B-A sú 2 rozdielne možnosti). Napríklad: Máme písmená A, B, C, D, E, F. Koľko máme možností výberu troch z nich ak záleží na poradí a v jednej možnosti môže byť každé písmeno ľubovoľne krát? Možností bude 216.
Kombinácie bez opakovania vyjadrujú počet možností výberu istého počtu objektov z istej množiny, pričom v jednom výbere môže byť jeden objekt maximálne raz a na poradí nezáleží (čiže A-B a B-A je jedna a tá istá možnosť). Napríklad: Máme písmená A, B, C, D, E, F. Koľko máme možností výberu troch z nich ak nezáleží na poradí a v jednej možnosti môže byť každé písmeno maximálne raz? Možností bude 16.
Kombinácie s opakovaním vyjadrujú počet možností výberu istého počtu objektov z istej množiny, pričom v jednom výbere môže byť jeden objekt ľubovoľne krát a na poradí nezáleží (čiže A-B a B-A je jedna a tá istá možnosť). Napríklad: Máme písmená A, B, C, D, E, F. Koľko máme možností výberu troch z nich ak nezáleží na poradí a v jednej možnosti môže byť každé písmeno ľubovoľne krát? Možností bude 55.
Faktoriál je matematická operácia, kde číslo n násobíme všetkými prirodzenými číslami nižšími ako n. Faktoriál vyznačujeme výkričníkom za číslom. Napríklad: 5!=5•4•3•2•1=120.
- vzorec pre výpočet permutácií bez opakovania je n! (ak je n počet objektov, ktoré usporadúvam).
- vzorec pre výpočet permutácií s opakovaním je nn (ak je n počet objektov, ktoré usporadúvam).
- vzorec pre výpočet variácií bez opakovania je n!/m! (ak je n počet možností z ktorých si vyberám a m počet možností z ktorých si nevyberám). Napríklad: mám na výber 10 druhov zmrzlín a chcem si vybrať jednu trojitú. Koľko možností mám, ak mi na poradí záleží a zo žiadnej zmrzliny si nechcem dať dvakrát? Keďže 10-3=7 (zo siedmych možností si nevyberám) Výpočet je 10!/7!=10•9•8•
7•6•5•4•3•2/7•6•5•4•3•2=10•9•8=720. - vzorec pre výpočet variácií s opakovaním je nm (ak je n počet možností z ktorých si vyberám a m počet výberov). Napríklad: mám na výber 10 druhov zmrzlín a chcem si vybrať jednu trojitú. Koľko možností mám, ak mi na poradí záleží a z každej zmrzliny si môžem dať dvakrát? Keďže 10-3=7 (zo siedmych možností si nevyberám) Výpočet je 103=1000.
Riešenie výpočtom: výpočet kombinácií
Kombinácie bez opakovania vypočítame tak, že celkový počet variácií vydelíme počtom premutácií jednej kombinácie. Napríklad: Mám na výber 10 druhov zmrzlín a chcem si vybrať jednu trojitú. Koľko možností mám, ak zo žiadnej nechcem mať dvakrát a na poradí nezáleží? Výpočet je 10•9•8/3•2•1=720/6=120. Na výber mám 120 možností.
Vzorec pre výpočet kombinácií s opakovaním je príliš zložitý a na základnej škole sa neučí.