Mocniny a odmocniny
 V jednej starej legende si vypýtal človek, ktorý vymyslel šach, od kráľa takúto odmenu: na prvé políčko šachovnice daj dve zlaté mince, na druhú štyri, na ďalšiu 4 a na každé ďalšie políčko dvojnásobný počet mincí, aký je na predchádzajúcom políčku. Koľko mincí bude na 6. políčku? Pri výpočte využijeme mocniny.
V jednej starej legende si vypýtal človek, ktorý vymyslel šach, od kráľa takúto odmenu: na prvé políčko šachovnice daj dve zlaté mince, na druhú štyri, na ďalšiu 4 a na každé ďalšie políčko dvojnásobný počet mincí, aký je na predchádzajúcom políčku. Koľko mincí bude na 6. políčku? Pri výpočte využijeme mocniny.
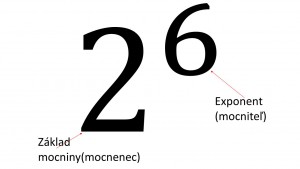
Umocňovanie je opakované násobenie. Napríklad 2•2•2•2•2•2=26=128 Na 6. políčku je teda 128 mincí. Základ mocniny(mocnenec) je číslo, ktoré sa opakovane násobí. Exponent(mocniteľ) je číslo ktoré určuje, koľkokrát sa základ násobí. Exponent zapisujeme horným indexom za základ mocniny.
Mocniny čítame tak, že najprv prečítame základ, potom povieme na a prečítame exponent ako radovú číslovku v štvrtom páde (akuzatíve). Napríklad 26 čítame ako dva na šiestu.
Kladné a záporné mocniny
Ak je pred mocninou znamienko, znamená to, že nie je súčasťou základu mocniny, ale znamienko výsledku mení na opačné. Napríklad -33=-27.
Ak chceme, aby znamienko bolo súčasťou mocniny, teda napríklad aby sme umocňovali záporné číslo, musíme ho dať do zátvorky spolu so základom. Napríklad (-3)3.
V takom prípade platia tieto pravidlá:
- Ak je exponent párny, výsledok je vždy kladný (t.j. (-5)2=25).
- Ak je exponent nepárny, výsledok má rovnaké znamienko ako mocnenec (t.j. (-3)3=-27).
- Akákoľvek mocnina čísla 0 sa rovná 0.
Druhá a tretia mocnina
Mocniny by sme počítali veľmi zdĺhavo, keby sme ich stále rozkladali na násobenie a to písomne počítali. No počítať mocniny sa dá aj inými spôsobmi, ktoré vám ukážem.
Je dobré zapamätať si druhú mocninu do 20 a tretiu mocninu do 10.
| a= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a2= | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 |
| a= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| a3= | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Druhá mocnina dvojnásobne zväčšuje počet núl aj počet desatinných miest (t.j. 1002=10000 a 0,012=0,0001). Tretia mocnina trojnásobne zväčšuje počet núl aj počet desatinných miest (t.j. 1003=1000000 a 0,013=0,000001). Z vyššie uvedených pravidiel vyplýva, že výsledok druhej mocniny je vždy kladný a výsledok tretej mocniny má rovnaké znamienko ako jej základ.
S využitím týchto pravidiel a matematických tabuliek (kde sú zväčša druhé a tretie mocniny do 1000) vieme určiť širokú škálu mocnín. Napríklad 451002 určíme takto: v tabuľke si zistíme, koľko je 4512(203401) a potom k tomu pridáme dvojnásobný počet núl. Takže 451002=2 034 010 000.
Ako však určiť mocninu čísla, ktorého nenulová časť nie je v tabuľkách? V takom prípade prípade ho zaokrúhlime tak, aby bola. Napríklad 224812 určíme takto: najprv ho zaokrúhlime na 22500, potom si v tabuľke zistíme druhú mocninu 225(50625) a pripíšeme dvojnásobný počet núl. Takže 224812≈506 250 000.
Vzorce pre úpravu výrazov s druhou mocninou
Pre úpravu výrazov s druhou mocninou máme vzorce. Dajú sa logicky odvodiť, v tomto príspevku to však robiť nebudem. Za a, b si môžem dosadiť akékoľvek premenné:
- (a•b)n=an•bn (a:b)n=an:bn
- (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
- a2-b2=(a+b)•(a-b)
Počítanie s mocninami, výrazy s mocninami
Sčítanie, odčítanie, násobenie a umocňovanie mocnín
Sčítame a odčítame len mocniny s rovnakým základom (premennou) aj exponentom. Tie sa nemenia, počítame iba s koeficientmi. Napríklad 4x3-x3=3x3.
Násobiť vieme mocniny s rovnakým základom. Teraz si skúsime odvodiť ako: je zadaný príklad x2•x3. Najprv si ho rozložíme na čisté násobenie (x•x•x•x•x) a potom to premeníme na mocninu(x6). Vidíme, že základ ostáva rovnaký, a exponenty sčítavame. V prípade, že pred mocninami sa nachádzajú ešte nejaké koeficienty, tie vynásobíme. Napr. 3x2•2x5=6x7
Umocňovanie mocnín sa robí tak, že sa exponenty navzájom násobia. Napr. (x3)4=x12.
Delenie mocnín a mocniny so záporným alebo nulovým exponentom
Ako násobiť, tak aj deliť vieme mocniny s rovnakým základom. Teraz si skúsime odvodiť ako: je zadaný príklad x6:x3. Najprv si mocniny rozložíme na násobenie a príklad zmeníme na zlomok (x•x•x•x•x•x/x•x•x). Potom vykrátime, čo sa dá (x•x•x•x•x•x/x•x•x=x•x•x/1=x•x•x) a výsledok zmeníme na mocninu(x3). Vidíme, že základ ostáva rovnaký a exponenty odčítavame.
Ale ako sa mocniny delia, keď je exponent delenca menší ako exponent deliteľa? Pokúsime sa to odvodiť: dáme si príklad x2:x5. Najprv si mocniny rozložíme na násobenie a príklad zmeníme na zlomok (x•x/x•x•x•x•x). Potom vykrátime, čo sa dá (x•x/x•x•x•x•x=1/x•x•x) a výsledok zmeníme na mocninu (1/x3). Ak však použijeme predchádzajúce pravidlo s odčítavaním (x2:x5=x2-5), tak nám vyjde x-3. Z toho vyplýva, že x-n=1/xn (t.j. x-3=1/x3).
Ak je exponent delenca rovnaký ako exponent deliteľa (základy sú samozrejme rovnaké tiež), tak sa navzájom vykrátia a vznikne 1. Ak však použijeme pravidlo odčítania, vznikne nám mocnina s exponentom 0. Z toho vyplýva, že akékoľvek číslo umocnené na nultú sa rovná 1.
Diskutabilný prípad je 00. Matematici sa nevedia dohodnúť, či sa to rovná 1(podľa pravidla, že akékoľvek číslo umocnené na nultú sa rovná 1) alebo či sa to rovná 0(podľa pravidla, že akákoľvek mocnina čísla 0 sa rovná 0).
Roznásobovanie výrazov s premennou výrazom
Výrazy s premennou roznásobujeme druhým výrazom tak, že všetky členy z prvého výrazu (v prvej zátvorke) vynásobíme všetkými členmi druhého výrazu (v druhej zátvorke).
Napríklad: (4x+5y)•(2x+3y+z)=8x2+12xy+4xz+10yx+15y2+5yz= =8x2+22xy+4xz+15y2+5yz.
Lomené výrazy a ich zjednodušovanie
Lomené výrazy sú výrazy, ktoré obsahujú premenné v menovateli. Lomené výrazy upravujeme tak, že najprv sa všetko sčítanie a odčítanie v nich snažíme premeniť na násobenie. To robíme pomocou vynímania pred zátvorku a vzorcov pre úpravu výrazov s druhou mocninou (pozri vyššie).
Uvediem vám jeden príklad úpravy lomeného výrazu: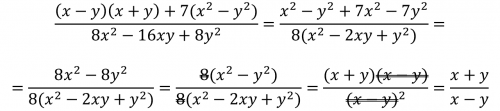
Odmocniny
Druhá a tretia odmocnina

Odmocňovanie je opakom umocňovania. ∛27=3, lebo 33=27.
Odmocniny sa väčšinou počítajú na kalkulačke, ale dajú sa aj spamäti a pomocou tabuliek. Ako, to napíšem v tomto príspevku.
Pre odmocniny poznáme tieto vzorce:
![]()
![]()
Ak sa naučíme druhé mocniny do dvadsať a tretie do desať, niektoré odmocniny vieme vypočítať spamäti.
Vzhľadom na to, že druhá odmocnina dvojnásobne zväčšuje a a tretia trojnásobne zväčšuje, tak druhá odmocnina dvojnásobne zmenšuje a tretia trojnásobne zmenšuje počet núl(t.j. √100=10 a ∛1000=10) aj počet desatinných miest(t.j. √0,01=0,1 a ∛0,001=0,1).
S využitím týchto pravidiel a matematických tabuliek (kde sú zväčša druhé a tretie mocniny do 1000) vieme určiť širokú škálu mocnín. Napríklad √45100 určíme takto: rozložíme si to na √451•√100. V tabuľke si zistíme, koľko je √451(približne 21,24). Vzhľadom na to, že druhá odmocnina dvojnásobne zmenšuje počet núl, tak √100=10. Desiatkou teda vynásobíme 21,24. Takže √45100≈212,4.
Ako však určiť odmocninu čísla, ktorého nenulová časť nie je v tabuľkách? V takom prípade prípade ho zaokrúhlime tak, aby bola. Napríklad √22481 určíme takto: najprv ho zaokrúhlime na 22500, potom si v tabuľke zistíme druhú odmocninu 225 (15) a vynásobíme desiatkou (lebo √100=10). Takže √22481≈150.
Existuje ešte tzv. čiastočné odmocnenie. Využívame ho, keď je výsledok odmocniny iracionálne číslo, pričom však vieme odmocnenca rozložiť na súčin tak, že jeden z činiteľov bude odmocniteľný. Napríklad druhá odmocnina z čísla 27: √27=√(9•3)=√9•√3=3•√3
Vyššie odmocniny a mocniny s necelým exponentom
Vyššie už bolo uvedené, že pri umocňovaní mocnín sa mocnitele násobia. Z toho môžeme vydedukovať, že pri opačnom procese, teda pri odmocňovaní mocnín sa bude mocniteľ deliť odmocniteľom. Čiže napríklad štvrtá odmocnina z x8 bude x8/4, čiže x2. Už teda vidíme, ako je definovaná mocnina s exponentom, ktorý je zlomok - ako odmocnina (s odmocniteľom rovným menovateľu) mocniny (s mocniteľom rovným čitateľu). Z tohto si môžeme odvodiť nasledovné vzorce:


Vedecký zápis čísel
Vedecký zápis čísel je zápis čísel pomocou desatinného čísla a mocniny čísla 10. Takže je zapísaný v tvare a•10n, pričom n musí byť celé číslo a a musí byť číslo menšie ako 10 a väčšie alebo rovné 1. Používa sa na vyjadrenie veľmi veľkého čísla (napr. 420000000=4,2•108) alebo veľmi malého čísla (napr. 0,0000056=5,6•10-6).
Ako číslo previesť na vedecký zápis? Tu je postup:
- V prípade veľmi veľkého čísla si opíšeme prvé číslice (až dokiaľ sa nezačnú opakované nuly). V prípade veľmi malého čísla si opíšeme posledné číslice (odkiaľ končia nuly). Z čísla 420000000 si opíšem 42. Z čísla 0,0000056 si opíšem 56.
- Napíšeme desatinnú čiarku za prvú číslicu opísanej časti čísla. Z čísla 42 bude 4,2 a z čísla 56 bude 5,6.
- Napíšeme •10 a k desiatke pripíšeme exponent. Tento exponent vyjadruje, o koľko miest musíme posunúť desatinnú čiarku, aby sme z vedeckého zápisu dostali normálny zápis. Kladný exponent píšeme, ak desatinnú čiarku posúvame doprava a záporný exponent, ak doľava. Aby som z 4,2 dostal 420000000, tak mi treba desatinnú čiarku posunúť o 8 miest doprava, takže vedecký zápis čísla 420000000 je 4,2•108. Aby som z 5,6 dostal 0,0000056, tak mi treba desatinnú čiarku posunúť o 6 miest doľava, takže vedecký zápis čísla 0,0000056 je 5,6•10-6.
Využitie vedeckého zápisu čísel pri rozklade čísel v desiatkovej sústave
Rozklad čísel vieme urobiť aj pomocou vedeckého zápisu. Robí sa to tak, že v rozklade desaťnásobky desiatky nahradíme mocninami desiatky (...stovky 102, desiatky 101, jednotky 100, desatiny 10-1, stotiny 10-2...). Napríklad 28203,875=2•104+8•103+2•102+0•101+3•100+8•10-1+7•10-2+5•10-3.