Lineárne nerovnice
Nerovnica je porovnanie dvoch výrazov pomocou týchto znamienok:
- < (je menšie ako)
- > (je väčšie ako)
- ≤ (je menšie, nanajvýš rovné ako)
- ≥ (je väčšie, nanajvýš rovné ako)
Lineárne nerovnice riešime podobne ako lineárne
rovnice, používame ekvivalentné úpravy. Ale pozor! Ak nerovnicu násobíme alebo delíme záporným číslom, tak znamienko nerovnosti musíme zmeniť na opačné! Rovnako otočíme znamienko nerovnosti pri výmene strán nerovnice.
Riešnie každej nerovnice nás dovedie k nerovnosti.
Nerovnosti. Kam s nimi?
Nerovnosti môžeme riešiť buď v obore (množine) prirodzených čísel (v N), alebo v obore (množine) celých čísel (v Z), alebo v obore (množine) reálnych čísel (v R). Riešenie (koreň) nerovnice zapisujeme ako K Є (koreň patrí do...).
Množiny a číselná os: riešenia v N a v Z
Je daná nerovnosť 2<x<10. Jej riešenie v množine prirodzených čísel môžeme zapísať do množinovej zátvorky, a to tak, že tam vypíšeme všetky možné riešenia. Čiže: K Є {3; 4; 5; 6; 7; 8; 9}.
Ale čo ak je nerovnosť priveľmi obsiahla a nám sa nechce vypisovať všetky možné rešenia? V takom prípade stačí napísať niekoľko okrajových čísel a medzi ne dať tri bodky. Napríklad zápis riešenia nerovnosti x≤5 v Z (v množine celých čísel) bude K Є {-∞...3; 4; 5}.
Na číselnej osi vyznačujeme riešenia tak, že na nej označíme všetky body z množiny. Ak ich je priveľa, tak zakreslíme časti číselnej osi s okrajovými riešeniami, medzi ktoré dáme tri bodky. Ak riešenia pokračujú do nekonečna (resp. začínajú od mínus nekonečna), tak nakreslíme časť číselnej osi s riešeniami a dáme za ňu (resp. pred ňu) tri bodky.
Intervaly a číselná os: riešenia v R
Ak rovnicu riešime v množine reálnych čísel (v R), tak nemôžeme vypísať v množinovej zátvorke všetky riešenia, lebo je ich nekonečne veľa. V takom prípade používame intervaly. Intervaly zaznačujeme okrúhlou alebo špicatou zátvorkou, do ktorej napíšeme okrajové čísla.
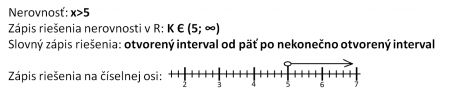
Otvorený interval (...; ...) používame, keď okrajové číslo nie je presne určené, napríklad x>5, čiže riešenia sú všetky čísla od 5 okrem 5 (aj 5,1; 5,001; atď). otvorený interval používame, aj keď je okrajové číslo nekonečno (resp mínus nekonečno).
Uzavretý interval 〈...; ...〉 používame, keď je okrajové číslo presne určené, napríklad 2≤x≤5, čiže riešenia sú všetky čísla od 2 do 5, vrátane 2 a 5.
Polootvorený (polouzavretý) interval používame, keď je jedno okrajové číslo presne určené a druhé nie. Napríklad 0≤x<7, čiže riešenia sú všetky čísla od 0 do 7, vrátane 0 a okrem 7.
Intervaly čítame takto: ,,otvorený/uzavretý interval od ... do/po ... otvorený/uzavretý interval".
Na číselnej osi riešenia v obore reálnych čísel vyznačujeme čiarou nad osou, ktorá medzi okrajovými číslami. Začína aj končí sa krúžkom. Krúžok je plný-vyfarbený, pokiaľ ide o uzavretý interval a prázdny-nevyfarbený, pokiaľ ide o otvorený interval. Ak je jedno okrajové číslo nekonečno (resp. mínus nekonečno), tak sa čiara končí (resp. začína) šípkou.
