Funkcie a lineárna funkcia
Funkcia je priradenie (vzťah), ktoré jednému číslu x priradí práve jedno číslo y.
|
|
|
|
|
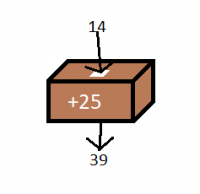
Funkcia je teda ,,akási zázračná škatuľka", do ktorej keď vhodím jedno číslo, tak mi vypadne druhé. |
|
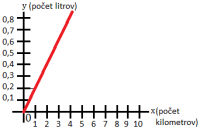
Slovne: Na 1 kilometer minie auto 0,2l benzínu. |
||||||||||||||
|
Rovnicou (kde je x počet kilometrov a y počet minutých litrov benzínu): y=0,2•x |
||||||||||||||
|
Grafom:
|
||||||||||||||
|
Tabuľkou:
|
Nezávislá premenná je premenná, ktorá spôsobuje daný efekt. Určujeme si ju sami. Najčastejšie ju označujeme x. V grafe ju vyjadruje o vodorovná os x. (Vo vyššie uvedenom príklade to je počet kilometrov).
Závislá premenná je premenná, ktorá sa mení vzhľadom k danej nezávislej premennej. Jej hodnotu nevieme nijako ovplyvniť (jedine zmenou hodnoty x). Najčastejšie ju označujeme y. V grafe ju vyjadruje zvislá os y. (Vo vyššie uvedenom príklade to je počet litrov).
Funkcia nemusí byť na grafe vždy priamka. Môže to byť aj polpriamka, úsečka alebo len body.
Definičný obor a obor hodnôt funkcie
Definičný obor funkcie je obor (množina) všetkých čísel, ktoré môžu byť nezávislou premennou (x). Definičný obor funkcie f označujeme ako D(f)=.
Obor hodnôt funkcie je obor (množina) všetkých čísel, ktoré môžu byť závislou premennou (y). Obor hodnôt funkcie f označujeme ako H(f)=.
Množiny a funkcie, ktorých grafom sú body
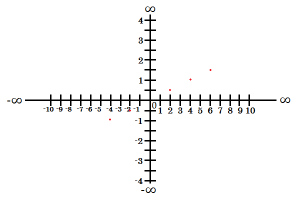
Definičný obor a obor hodnôt funkcií, ktorých grafom sú body zapisujeme pomocou množiny. Zapisujeme to tak, že do množinovej zátvorky zapíšeme všetky možné riešenia. V prípade, že je ich priveľa, tak stačí napísať okrajové riešenia a medzi ne dať tri bodky.
|
D(f)={-4; -2; 0; 2; 4; 6} H(f)={-1; -0,5; 0; 0,5; 1; 1,5}
|
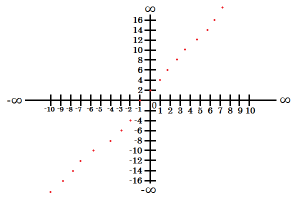
|
D(f)={-∞...-2; -1; 0; 1; 2...∞} H(f)={-∞...-6; -4; -2; 0; 2; 4...∞} |
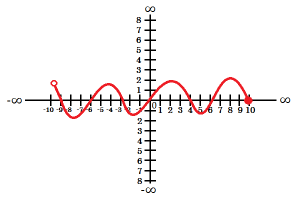
Intervaly a funkcie, ktorých grafom je čiara
Ak je grafom funkcie čiara, tak nemôžeme do množinovej zátvorky vypísať definičný obor, ani obor hodnôt, lebo by obsahoval nekonečne veľa čísel. V takom prípade používame intervaly.
Otvorený interval (...; ...) používame, keď okrajové číslo nie je presne určené, napríklad x>5, čiže riešenia sú všetky čísla od 5 okrem 5 (aj 5,1; 5,001; atď). Na grafe sa to znázorňuje prázdnym krúžkom ukončujúcim čiaru. Otvorený interval používame, aj keď je okrajové číslo nekonečno (resp. mínus nekonečno).
Uzavretý interval 〈...; ...〉 používame, keď je okrajové číslo presne určené, napríklad x≤15, čiže riešenia sú všetky čísla do 15 vrátane 15. Na grafe sa to znázorňuje plným krúžkom ukončujúcim čiaru.
Intervaly čítame takto: ,,otvorený/uzavretý interval od ... do/po ... otvorený/uzavretý interval".
|
D(f)=(-10; 10〉 H(f)=〈-2; 2〉
|
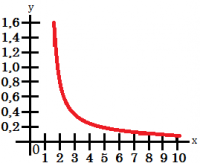
|
D(f)=(0; ∞) H(f)=(0; ∞) |
Lineárna funkcia
Lineárna funkcia je každá funkcia s predpisom y=k•x+q, kde k a q sú ľubovoľné reálne čísla. Grafom lineárnej funkcie je priamka.
Lineárna funkcia môže byť:
|
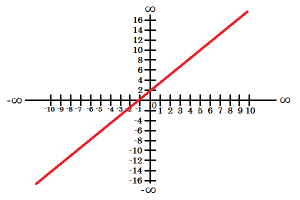
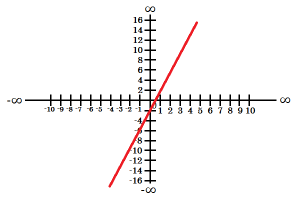
I.rastúca -ak k>0 -predpis funkciu vľavo je f: y=2x+2 |
|
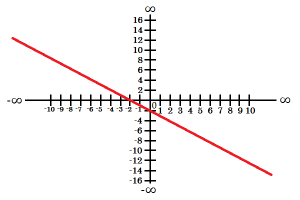
-ak k<0 -predpis pre funkciu vľavo je f: y=-x-2
|
|
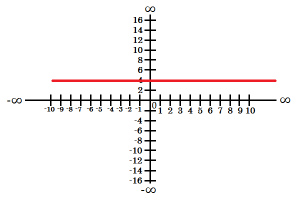
-ak k=0 -predpis pre funkciu vľavo je f: y=0x+4=4 |
Priesečníky grafu lineárnej funkcie s osami x a y
Graf lineárnej funkcie pretína os y v bode [0; q], čiže v bode osi y kde sa hodnota y rovná konštante q.
Priesečník grafu lineárnej funkcie s osou x určíme tak, že za y si dosadíme nulu a vyriešime rovnicu.
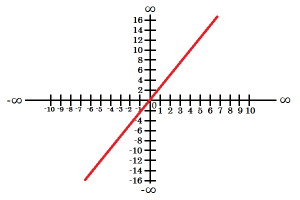
Príklad: Je daná funkcia s predpisom y=2x-1. Urči priesečníky jej grafu s osami x a y! q=-1, čiže priesečník s osou y bude v bode [0; -1]. Keď vyriešime rovnicu 0=2x-1, vyjde nám x=0,5. Čiže priesečník s osou x je v bode [0,5; 0]. Keď už poznáme 2 body priamky, tak vieme narysovať aj graf.
 |
|
|