Desatinné čísla
Mnohí z vás chodia nakupovať, niekedy s rodičmi, kamarátmi alebo aj sami. Ceny takmer všetkých tovarov sú udávané číslami, ktoré obsahujú medzi číslicami aj čiarku. Takéto čísla nazývame desatinné čísla a čiarka, ktorá v nich je desatinná čiarka. Desatinné číslo poznáme podľa toho, že obsahuje desatinnú čiarku.
Desatinné čísla sú čísla, ktoré sa nachádzajú medzi celými číslami. Desatinná čiarka ho rozdeľuje na dve časti: celá časť sú číslice pred desatinnou čiarkou(vľavo od nej). Desatinná časť sú číslice za desatinnou čiarkou(vpravo od nej). V celej časti sú jednotky, desiatky, stovky atď. V desatinnej časti sú desatiny, stotiny, tisíciny atď.
Numerácia desatinných čísel
Čítanie desatinných čísel
1.Najprv prečítame celú časť. Aby sme vedeli, kde sa končí, tak po jej dočítaní povieme celá, celých alebo celé. Ak má celá časť hodnotu nula, povieme celých. Ak jedna, povieme celá. Ak dva, tri, alebo štyri, povieme celé. Ak päť alebo viac, povieme celých.
2.Po prečítaní celej časti prečítame desatinnú časť. Aby sme vedeli, na ktorých desatinných miestach s číslice nachádzajú, tak nakoniec povieme názov desatiného miesta, na ktorom sa nachádza posledná prečítaná číslica. Názov desatinného čísla povieme v druhom páde-genitíve(má koncovku -in).
Takže číslo 6 132, 628 35 prečítame ako šesťtisíc stotridsaťdva celých šesťdesiatdvatisíc osemstotridsaťpäť stotisícin. Číslo 0,205 prečítame ako nula celých dvestopäť tisícin.
Zápis desatinných čísel na číselnej osi
Desatinné čísla zapisujeme na číselnej osi tak, že sú medzi celými číslami. Ak chceme zapísať nejaké desatinné číslo, úsek medzi danými celými číslami rozdelíme na desať častí, ak je potrebné tak na sto, alebo tisíc atď. Poradie daného dieliku za celým číslom je hodnota číslic za desatinnou čiarkou.
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3 | |
| 0,98 | 0,99 | 1 | 1,01 | 1,02 | 1,03 | 1,04 | 1,05 | 1,06 | 1,07 | 1,08 | 1,09 | 1,1 | 1,11 | 1,12 | 1,13 | 1,14 | 1,15 | 1,16 | 1,17 | 1,18 | 1,19 | 1,2 | 1,21 | 1,22 | 1,23 | 1,24 | 1,25 | 1,26 | 1,27 | 1,28 |
Porovnávanie a zaokrúhľovanie desatinných čísel
Desatinné čísla nemôžeme porovnávať tak ako prirodzené, lebo to, že je dlhšie nemusí znamenať, že je aj väčšie. Desatinné čísla porovnávam tak, že najprv porovnám celú časť s celou časťou, ak sú rovnaké, tak porovnávam desatiny s desatinami, ak sú rovnaké, tak porovnávam stotiny so stotinami. A tak pokračujem, až kým nezistím, ktoré číslo je väčšie. Napr.: 253,541<253,56 0,64>0,5
Pri zaokrúhľovaní desatinných čísel platí rovnaký princíp, ako pri zaokrúhľovaní prirodzených. Ak chceme číslo zaokrúhliť na nejaké miesto, tak si pozrieme či má nasledujúce miesto hodnotu menšiu ako päť alebo nie. Ak má menšiu, číselná hodnota miesta, na ktoré zaokrúhľujeme, sa nezmení. Ak je rovnaká alebo väčšia, tak sa zväčší o 1. Napríklad zaokrúhlenie na stotiny: 25,7418≈25,74 14,645≈14,65.
Počtové operácie s desatinnými číslami
Sčítanie a odčítanie desatinných čísel
Desatinné čísla písomne sčítavame a odčítavame rovnako ako prirodzené, ale desatinná čiarka ako aj číslice rovnakého rádu pred ňou aj za ňou musia byť pod sebou na rovnakých miestach. Takže desatiny budú po desatinami, stotiny pod stotinami atď.


Násobenie desatinných čísel
Desatinné čísla násobíme písomne rovnako ako prirodzené. Počet desatinných miest vo výsledku sa bude rovnať súčtu počtov desatinných čísel v oboch činiteľoch.

Číslo sa zmenší, ak ho násobím desatinným číslom menším ako 1. Číslo sa zväčší, ak ho násobím číslom väčším ako 1. Pri násobení čísel desaťnásobkami desiatky(10, 100, 1000...) iba posúvam desatinnú čiarku doprava o toľko miest, koľko núl má desaťnásobok desiatky, ktorý je činiteľom (napr. 45,824x100=4582,4). Pri násobení čísel číslami 0,1 0,01 0,001 atď. iba posúvam desatinnú čiarku doprava o toľko miest, koľko miest má dané číslo, ktoré je činiteľom (napr. 45,824x0,01=0,45824).
Delenie desatinných čísel
Desatinné čísla písomne delíme rovnakým princípom ako prirodzené, ale platia tu isté pravidlá:
 1.Ak chceme pokračovať v delení dvoch prirodzených čísel, v ktorom vyšiel zvyšok, tak do výsledku zapíšeme desatinnú čiarku, a pokračujeme v delení. Do zvyšku pripíšeme nulu a toto číslo delíme.
1.Ak chceme pokračovať v delení dvoch prirodzených čísel, v ktorom vyšiel zvyšok, tak do výsledku zapíšeme desatinnú čiarku, a pokračujeme v delení. Do zvyšku pripíšeme nulu a toto číslo delíme.
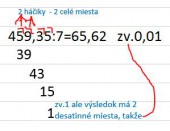 2.Ak delíme delenca, ktorý je desatinným číslom a deliteľ je prirodzeným číslom, tak po prekročení desatinnej čiarky v delenci napíšeme desatinnú čiarku aj do výsledku a pokračujeme ďalej v delení. Ak vydelíme už aj poslednú číslicu delenca a ešte nemáme úplný podiel, tak buď pokračujeme v delení podľa pravidla 1(pridávame do zvyšku nulu), alebo zapíšeme zvyšok. Zvyšok však musí mať toľko desatinných miest, koľko desatinných miest má výsledok.
2.Ak delíme delenca, ktorý je desatinným číslom a deliteľ je prirodzeným číslom, tak po prekročení desatinnej čiarky v delenci napíšeme desatinnú čiarku aj do výsledku a pokračujeme ďalej v delení. Ak vydelíme už aj poslednú číslicu delenca a ešte nemáme úplný podiel, tak buď pokračujeme v delení podľa pravidla 1(pridávame do zvyšku nulu), alebo zapíšeme zvyšok. Zvyšok však musí mať toľko desatinných miest, koľko desatinných miest má výsledok.
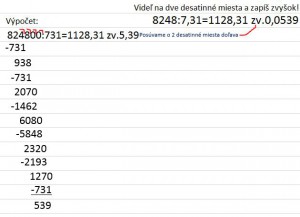 3.Ak je desatinné číslo deliteľom, tak si ho vynásobíme desaťnásobkom desiatky tak, aby už desatinné nebolo. Ale potom si rovnakým desaťnásobkom desiatky musíme vynásobiť aj delenca. Ak však potom chceme napísať desatinný zvyšok, musíme si ho vydeliť rovnakým desaťnásobkom desiatky, akým sme vynásobili príklad. Takže o koľko desatinných miest doprava sa posunula desatinná čiarka v delenci, o toľko desatinných miest doprava musíme posunúť desatinnú čiarku vo zvyšku.
3.Ak je desatinné číslo deliteľom, tak si ho vynásobíme desaťnásobkom desiatky tak, aby už desatinné nebolo. Ale potom si rovnakým desaťnásobkom desiatky musíme vynásobiť aj delenca. Ak však potom chceme napísať desatinný zvyšok, musíme si ho vydeliť rovnakým desaťnásobkom desiatky, akým sme vynásobili príklad. Takže o koľko desatinných miest doprava sa posunula desatinná čiarka v delenci, o toľko desatinných miest doprava musíme posunúť desatinnú čiarku vo zvyšku.
4.Pri delení sa môže stať, že sa istá číslica(alebo viac číslic) bude opakovať do nekonečna. Ak sa to stalo napíšeme nad ňu(nich) vodorovnú čiaru. Keď čítame takýto výsledok, doplníme zaň slovo periodických. Napríklad ![]()
Číslo sa zväčší, ak ho delím desatinným číslom menším ako 1. Číslo sa zmenší, ak ho delím číslom väčším ako 1. Pri delení čísel desaťnásobkami desiatky(10, 100, 1000...) iba posúvam desatinnú čiarku doľava o toľko miest, koľko núl má daný desaťnásobok desiatky (napr. 45,824:100=0,45824). Pri delení čísel číslami 0,1 0,01 0,001 atď. posúvam desatinnú čiarku o toľko miest, koľko miest má dané číslo, ktoré je činiteľom (napr. 45,824:0,01=4582,4).
Aritmetický priemer
Aritmetický priemer sa počíta tak, že spočítame hodnoty všetkých čísel, na ktoré ho počítame a potom ten súčet vydelíme počtom čísel, na ktoré aritmetický priemer počítame.
Takže napríklad z matematiky som dostal tieto známky: 2; 3; 1; 2; 2; 4; 3; 2; 1; 2. Chcem si vypočítať ich priemer. Najprv sčítam ich hodnoty: 2+3+1+2+2+4+3+2+1+2=22. Počet známok je 10 a preto vydelím 22:10=2,2. Priemer mojich známok je 2,2.