Mechanika: tlak a vztlak
Na vyjadrenie účinkov sily pôsobiacej kolmo na plochu, ako aj na opis silového pôsobenia v kvapalinách a plynoch a na vyjadrenie miery deformácie telies z tuhých látok používame fyzikálnu veličinu tlak (značka p z anglického ,,pressure"). Tlak priamoúmerne závisí od sily pôsobiacej kolmo na plochu (tzv. tlakovej sily) a nepriamoúmerne od obsahu tej plochy. Vypočítame ho teda ako podiel tlakovej sily a obsahu plochy, na ktorú pôsobí (p=F/S). Tlaková sila má v telesách z tuhých látok deformačné účinky. Jednotka tlaku je pascal. Keďže tlak vypočítame ako podiel sily (v newtonoch) a obsahu (v metroch štvorcových), tak pascal je vlastne newton na meter štvorcový (N/m2=N•m-2). Keďže tlak nepriamoúmerne závisí od plochy, tak sa nám lepšie krája ostrými nožmi (ich hrana je veľmi tenká, čiže má len malú plochu a teda aj malou silou vieme vyvinúť veľký tlak. Na rovnakom princípe sa dá vysvetliť, prečo na prepichovanie používame ihlu, prečo sa vieme porezať na ostrých predmetoch alebo prečo si máme ľahnúť, ak sme v strede zamrznutého jazera a ľad začína pukať (zväčšíme plochu, zmenšíme tlak).
Prístroj na meranie tlaku sa nazýva manometer alebo tlakomer. Poznáme veľa druhov (aneroid, vákuometer, manovákuometer, barometer...) tlakomerov na meranie rôznych tlakov.
Vyrieš príklady (správne riešenia sú na konci príspevku):
1.) Plocha podrážky mojej topánky má veľkosť 270cm2, vážim 80kg a meriam 185cm. O koľko menší tlak bude moja noha vyvíjať ak je nasadená v lyži, ak má lyža šírku 86cm, stojím na oboch nohách a dĺžka lyže je o 7cm menšia ako moja výška? Pre zjednodušenie považujte lyže za obdĺžniky a počítajte so zaokrúhlenou hodnotou tiažového zrýchlenia (10N•kg-1).
2.) Medza pevnosti v tlaku menej kvalitného betónu je 18MPa a jeho hustota je 2400kg•m-3. Dovoľujú bezpečnostné predpisy postaviť z neho 300m vysoký televízny stožiar, ak je tlaková miera bezpečnosti 3? (Poznámka: Medza pevnosti v tlaku znamená maximálny tlak, pri ktorom sa ešte nerozpadne. Tlaková miera bezpečnosti rovná 3 znamená, že pre bezpečnosť stavba nesmie byť podľa bezpečnostných predpisov pod väčším tlakom ako jedna tretina tlaku, ktorý by teoreticky vedel vydržať.)
Sily pôsobiace v tekutinách (kvapalinách a plynoch)
Tlak v kvapalinách (hydrostatický tlak)
Celkový tlak na určitom mieste kvapaliny, ktorá je v pokoji, je súčtom troch čiastkových (parciálnych) tlakov: atmosférický tlak, tlak vyvolaný vonkajšou silou a hydrostatický tlak. O atmosférickom tlaku píšem nižšie. Čo sa týka tlaku vyvolaného vonkajšou silou, tak preňho platí pascalov zákon: tlak vyvolaný vonkajšou silou pôsobiacou na povrch kvapaliny, je na všetkých jej miestach rovnaký.
Hydrostatický tlak (ph) je tlak vyvolaný tiažou kvapaliny (tiažovou silou, ktorou na ňu Zem pôsobí). Horné častice kvapaliny tlačia na dolné častice kvapaliny a spolu tlačia na predmety ponorené v kvapaline a dno nádoby. Tlaková sila je v tomto prípade totožná s tiažovou silou. Pokúsme sa odvodiť vzorec na výpočet hydrostatického tlaku: Pre jednoduchosť budeme počítať hydrostatický tlak, ktorým kvapaliny pôsobí na dno nádoby. Základný vzorec na výpočet tlaku je p=F/S. Keďže tlaková sila je tu totožná s tiažovou, môžeme si do vzorca na výpočet tlaku dosadiť namiesto tlakovej sily vzorec na výpočet tiažovej sily (FG=m•g) a dostaneme vzorec p=m•g/S. Za hmotnosť si môžeme dosadiť ρ•V, takže dostaneme p=ρ•V•g/S. Objem a obsah sa nám navzájom vykrátia za vzniku dĺžky (v tomto prípade hĺbky, h), čiže výsledný vzorec na výpočet tlaku bude ph=h•ρ•g. Ako vidíme, hydrostatický tlak nezávisí od množstva kvapaliny, ale iba od hĺbky ponoru. Tento jav sa nazýva hydrostatický paradox.
Vyrieš príklady (správne riešenia sú na konci príspevku):
3.) Najhlbšie miesto na Zemi je Mariánska priekopa v Tichom oceáne. Jej dno leží v hĺbke 11km. Vypočítaj, aký tlak na jej dne je, ak má morská voda hustotu 1030kg•m-3.
4.) Do akej hĺbky sa dokáže bezpečne ponoriť ponorka, ktorá dokáže zniesť tlak bezpečne maximálne 50MPa? Ponára sa v mori a my vieme, že hustota morskej vody je 1030kg•m-3.
Atmosférický tlak
Atmosférický tlak (p) je tlak vzduchu vyvolaný jeho tiažou (tiažovou silou, ktorou naň Zem pôsobí). Horné častice vzduchu tlačia na predmety, ktoré sa v ňom nachádzajú a na povrch Zeme. S nadmorsskou výškou klesá. Atmosférický tlak sa mení v závislosti od počasia od 970hPa po 1055hPa. Atmosférický tlak sa pri predpovediach počasia uvádza v hektopascaloch, lebo kedysi bolo zaužívané udávať ho v milibaroch (bar je stará jednotka tlaku zodpovedajúca stotisíc pascalom). Potom bolo nariadené, aby sa prešlo na jednotky zo sústavy SI. Aby si ľudia nemuseli zvykať na nové hodnoty, tak sa začali používať jednotky zo sústavy SI, ktoré majú rovnakú hodnotu ako milibary - čiže hektopascaly.
Vypočítať atmosférický tlak je zložité a neučí sa to ani na základnej, ani na strednej škole. Za normálny atmosférický tlak pri hladine mora sa považuje tlak 101325Pa.
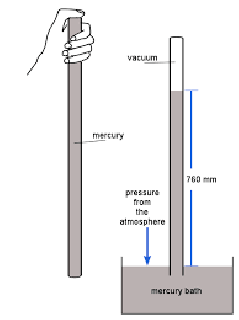Prvé meranie atmosférického tlaku vykonal v 17. storočí Torricelli, ktorý aj zostrojil prvý barometer. Zostrojil ho tak, že vzal 1m dlhú tenkú sklenenú trubicu na jednom konci uzavretú a po okraj ju naplnil ortuťou. Potom ju zapchal prstom aj na druhej strane, otočil do zvislej polohy (otvorený koniec, ktorý bol zapchatý len prstom smeroval nadol) a ponoril do nádoby s ortuťou. Časť ortuti stiekla do nádoby, ale časť ostala v rúrke. Nad ortuťou v rúrke vzniklo vzduchoprázdno - vákuum (v skutočnosti to však úplné vákuum nebolo, lebo obsahovalo isté množstvo ortuťových pár). Tomu, aby všetka ortuť stiekla, bránil atmosférický tlak, ktorý tlačil na ortuť nádobe a tá potom vytláčala ortuť v rúrke smerom nahor. Ortuť vystúpila vyššie, keď bol tlak vyšší a zostúpila nižšie, keď bol tlak nižší. Hydrostatický tlak ortuti na dolnom konci rúrky sa rovná atmosférickému tlaku.
Možno sa pýtate, či by sa namiesto ortuti nedala použiť aj iná kvapalina. Dala, ale bolo by to náročnejšie. Väčšina ostatných kvapalín má nižšiu hustotu ako ortuť (sú teda ľahšie), a preto na nich pôsobí menšia tiažová sila, ktorá pri 1m dlhých rúrkach nestačí na to, aby vyrovnala silu atmosférického tlaku. Museli by sme teda použiť rúrku oveľa dlhšiu (napríklad pri vode aspoň 13m), čo by bolo nepraktické.
S ortuťovým tlakomerom súvisí ešte jedna jednotka tlaku, ktorá sa používa hlavne v medicíne na meranie krvného tlaku. Touto veličinou je Torr (Tor). Predstavuje jeden milimeter ortuťového stĺpca v tlakomery. Jej značka je Torr alebo Tor, alebo mmHg. Jeden Torr je približne 133,322Pa.
Vyrieš príklady (správne riešenia sú na konci príspevku):
5.) Hustota ortuti je 13534kg•m-3. Do akej výšky vystúpi ortuť v Torriceliho barometri pri normálnom atmosférickom tlaku?
6.) Akú výšku by musela mať rúrka Torricelliho barometra, ak by bol naplnený vodou namiesto ortuti a chceli by sme, aby vedel odmerať rovnaký maximálny atmosférický tlak, ako ortuťový Torricelliho barometer s rúrkou vysokou 1m?
Vztlaková sila, vztlak a archimedov zákon
Pri hustote som opísal, že z archimedovho zákona vyplýva, že teleso s väčšou hustotou ako kvapalina sa ponorí, teleso z menšou hustotou bude plávať a teleso s rovnakou hustotou sa bude vznášať. Čo ale ten archimedov zákon vlastne je?
Najprv si niečo povieme o vztlakovej sile. Vztlaková sila (FVZ) je sila, ktorá pôsobí na teleso v tekutine a pôsobí v opačnom smere ako tiažová (resp. gravitačná) sila (čiže je to sila, ktorá teleso ,,nadnáša" - tlačí smerom nahor). Vzniká preto, lebo v dôsledku tiažovej (resp. gravitačnej) sily je hydrostatický tlak na nižšie položenom mieste tekutiny väčší ako na vyššie položenom. Tlak kvapaliny teda vytláča teleso nahor. Vztlakovú silu môžeme vysvetliť aj ako dôsledok toho, že tiažová (resp. gravitačná) sila pôsobí na kvapalinu, v dôsledku čoho sa snaží dostať nadol, a preto vytláča teleso, ktoré jej v tom bráni.
Ale ako veľkosť vztlakovej sily vypočítať? Archimedov zákon znie tak, že teleso ponorené v tekutine je nadľahčované vztlakovou silou, ktorej veľkosť sa rovná tiaži rovnakého objemu kvapaliny, aký je objem ponorenej časti telesa (FVZ=FG; Vkvap.=Vteleso). Na základe tohto zákona si odvodíme vzorec: vzorec pre tiaž je FG=m•g. Do tohto vzorca si za hmotnosť dosadíme vzorec na jej výpočet z objemu (m=ρ•V) a dostaneme FVZ=ρ•Vk•g.
Ak teleso pláva, znamená to, že tiažová (resp. gravitačná) sila je vyrovnaná z tiažovou. Aby sa to dosiahlo, časť telesa je ponorená a časť je nad hladinou, keďže veľkosť vztlakovej sily priamoúmerne závisí od objemu ponorenej časti telesa.
Vyrieš príklady (správne riešenia sú na konci príspevku):
7.) Akú silu nám treba na zdvihnutie kameňa vo vode, ak je jeho objem 6dm3 a hmotnosť 15kg?
8.) Drevený klát plávajúci na vode má ponorené 2/3 svojho objemu. Aká je hustota dreva, z ktorého je klát vyrobený?
|
1.) Zadanie: Plocha podrážky mojej topánky má veľkosť 270cm2, vážim 80kg a meriam 185cm. O koľko menší tlak bude moja noha vyvíjať ak je nasadená v lyži, ak má lyža šírku 86cm, stojím na oboch nohách a dĺžka lyže je o 7cm menšia ako moja výška? Pre zjednodušenie považujte lyže za obdĺžniky a počítajte so zaokrúhlenou hodnotou tiažového zrýchlenia (10N•kg-1)
Zápis:
Výpočet: Najprv vypočítame tlak nohy v topánke. Tlak je podiel tlakovej sily, ktorá je v tomto prípade totožná s tiažovou (ktorú vypočítame ako súčin hmotnosti a tiažového zrýchlenia), ale keďže sa hmotnosť rozloží na obe nohy, tak hmotnosť vyvolávajúca silu v jednej nohe bude len polovičná: p1=F/S=m•g/2•S=80
Potom vypočítame rovnakým spôsobom tlak nohy v lyži. Keďže lyžu považujeme pre zjednodušenie za obdĺžnik, jej plocha sa bude rovnať súčinu jej dĺžky a šírky: p1=F/S=m•g/2•S=m•g/2•a•b=80
Nakoniec vypočítame rozdiel tlakov: Δp=p1-p2=14,81kPa-0,2613kPa=14,5487kPa≈14,5kPa
Odpoveď: Ak je moja noha nasadená v lyži, bude vyvíjať tlak menší približne o 14,5kPa. |
|
2.) Zadanie: Medza pevnosti v tlaku menej kvalitného betónu je 18MPa a jeho hustota je 2400kg•m-3. Dovoľujú bezpečnostné predpisy postaviť z neho 300m vysoký televízny stožiar, ak je tlaková miera bezpečnosti 3? (Poznámka: Medza pevnosti v tlaku znamená maximálny tlak, pri ktorom sa ešte nerozpadne. Tlaková miera bezpečnosti rovná 3 znamená, že pre bezpečnosť stavba nesmie byť podľa bezpečnostných predpisov pod väčším tlakom ako jedna tretina tlaku, ktorý by teoreticky vedel vydržať.)
Zápis:
Výpočet: Budeme počítať tlak na mieste, kde je najvyšší, aby sme si boli istý, že celý stožiar vydrží. Tlak je najvyšší úplne pri zemi, kde tlačí celá hmotnosť stožiara. Vzorec na výpočet tlaku je p=F/S. Tlaková sila sa bude rovnať tiažovej, čiže ju vypočítame ako súčin tiažového zrýchlenia a hmotnosti. Hmotnosť nepoznáme, tak si ju vyjadríme ako súčin objemu a hustoty. Vo vzorci už máme podiel objemu a obsahu. predpokladáme, že stožiar má tvar kvádra, hranola alebo valca a v tom prípade sa podiel objemu a obsahu podstavy bude rovnať výške. Teraz už môžeme počítať: p=F/S=m•g/S=ρ• p=2400
Medza pevnosti v tlaku menej kvalitného betónu je 18MPa, čiže je taký tlak by teoreticky vedel vydržať. Keďže je medza bezpečnosti 3, stavba musí byť pod menším tlakom ako je tretina medze pevnosti. Vydelíme si ju teda tromi: 18MPa/3=6MPa 7,063MPa>6MPa
Odpoveď: Keďže tlak je o niečo väčší ako tretina medze pevnosti, bezpečnostné predpisy nedovoľujú postaviť 300m vysoký televízny stožiar z menej kvalitného betónu, aj keď pravdepodobne by sa nezrútil. |
|
3.) Zadanie: Najhlbšie miesto na Zemi je Mariánska priekopa v Tichom oceáne. Jej dno leží v hĺbke 11km. Vypočítaj, aký tlak na jej dne je, ak má morská voda hustotu 1030kg•m-3.
Zápis:
Výpočet: ph=h•ρ•g ph=11000 ph=111147300Pa=111,1473MPa
Odpoveď: Tlak na dne Mariánskej priekopy je 111,1473MPa. |
|
4.) Zadanie: Do akej hĺbky sa dokáže bezpečne ponoriť ponorka, ktorá dokáže zniesť tlak bezpečne maximálne 50MPa? Ponára sa v mori a my vieme, že hustota morskej vody je 1030kg•m-3.
Zápis:
Výpočet: h=ph/ρ•g=50000000
Odpoveď: Maximálna hĺbka, do akej sa ponorka dokáže bezpečne ponoriť je 4,948km. |
|
5.) Zadanie: Hustota ortuti je 13534kg•m-3. Do akej výšky vystúpi ortuť v Torriceliho barometri pri normálnom atmosférickom tlaku?
Zápis:
Výpočet: h=ph/ρ•g=101325
Odpoveď: Pri normálnom atmosférickom tlaku vystúpi ortuť v Torricelliho barometri do výšky 76,32cm. |
|
6.) Zadanie: Akú výšku by musela mať rúrka Torricelliho barometra, ak by bol naplnený vodou namiesto ortuti a chceli by sme, aby vedel odmerať rovnaký maximálny atmosférický tlak, ako ortuťový Torricelliho barometer s rúrkou vysokou 1m?
Výpočet: Najprv si vypočítame maximálny tlak odmerateľný ortuťovým barometrom s 1m vysokou rúrkou: p=h(Hg)•ρ(Hg)•g=1
Potom si výšku vodného stĺpca pri vypočítanom tlaku, čiže výšku rúrky: h(H2O)=p/ρ(H2O)•g=132768,54
Druhá (a podľa mňa jednoduchšia) možnosť výpočtu je pomocou trojčlenky, keďže pri rovnakom tlaku a tiažovom zrýchlení platí medzi hustotou a výškou stĺpca (hĺbkou) nepriama úmernosť: ⇩13534kg•m-3............................1m⇧ ⇩1000kg•m-3.................................x⇧ h(H2O)=13534
Odpoveď: Ak by bol Torricelliho barometer naplnený vodou namiesto ortuti a chceli by sme, aby vedel odmerať rovnaký atmosférický tlak ako ortuťový Torricelliho barometer s výškou rúrky 1m, tak by musel mať rúrku vysokú 13,534m. |
|
7.) Zadanie: Akú silu nám treba na zdvihnutie kameňa vo vode, ak je jeho objem 6dm3 a hmotnosť 15kg?
Zápis:
Výpočet: F=FG-FVZ=m•g-V•ρ(H2O)•g F=6 F=88,29N
Odpoveď: Na zdvihnutie kameňa vo vode je potrebná sila 88,29N. (V skutočnosti na začiatku je potrebné vynaložiť o máličko väčšiu silu, aby sa kameň pohol a až potom na udržanie kameňa v pohybe stačí sila 88,29N.) |
|
8.) Zadanie: Drevený klát plávajúci na vode má ponorené 2/3 svojho objemu. Aká je hustota dreva, z ktorého je klát vyrobený?
Zápis:
Výpočet: Vieme, že tiažová a vztlaková sila sa rovnajú. Na vytvorenie vzorca na výpočet hustoty dreva si teda vytvoríme rovnicu: FG=FVZ m•g=2/3V•ρ(H2O)•g V•ρ(drevo)•g=2/3V•ρ(H2O)•g /:(V•g) ρ(drevo)=2/3ρ(H2O) ρ(drevo)=2/3ρ(H2O)=2/3•1000kg•m-3≈666,7kg•m-3
Odpoveď: Hustota dreva, z ktorého je vyrobený klát, je 666,7kg•m-3. |
(Späť k príkladom sa dostanete kliknutím na číslo príslušného príkladu.)