Mechanika: sila, tiažová sila a trenie
Pôsobenie telies je vždy vzájomné (čiže keď vám dám facku, vaše líce vyvíja rovnakú silu na moju ruku ako moja ruka na vaše líce, ale keďže líce je jemnejšie, bolesť budete cítiť vy). Vzájomné pôsobenie telies sa môže uskutočniť buď vzájomným dotykom telies, alebo prostredníctvom fyzikálneho poľa (poznáme 3 druhy fyzikálneho poľa: gravitačné, elektrické a magnetické). Dôsledkom vzájomného pôsobenia telies môže byť buď deformácia alebo zmena pohybového stavu (uvedenie do pohybu, zastavenie, zmena rýchlosti alebo zmena smeru).
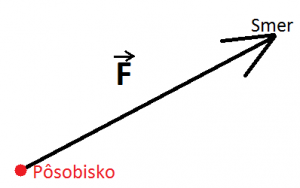Vzájomné pôsobenie telies opisujeme pomocou fyzikálnej veličiny sila (F). Jej jednotkou je newton (N). Bod, v ktorom sa účinky sily (deformácia, zmena pohybového stavu) bezprostredne uplatňujú, sa nazýva pôsobisko sily. Sila je však tzv. vektorová veličina, čo znamená, že okrem veľkosti je určená aj smerom. Silu znázorňujeme, rovnako ako všetky vektorové veličiny, orientovanou úsečkou (vektorom). Dĺžka vektora zodpovedá veľkosti sily (určíme si napríklad, že 1cm zodpvedá 1N), smer vektora zodpovedá smeru sily a začiatočný bod vektora vyjadruje pôsobisko sily. Značka sily je veľké F (z anglického ,,force"), ale keďže je sila vektorová veličina, píšeme nad značku ešte šípku. Avšak šípku nepíšeme v prípade, ak je pre danú úlohu podstatná iba veľkosť sily a nie smer.
Silu meriame pomocou silomera. Silomer sa skladá z pružiny, stupnice a obalu. Meranie sily silomerom je založené na priamej úmernosti predĺženia pružiny a pôsobiacej meranej sily (F~Δl). Keďže všeobecná rovnica (vzorec) priamej úmernosti je y=k•x, vzorec na výpočet sily pomocou predĺženia pružiny bude F=k•Δl. Konštanta úmernosti k je fyzikálna veličina charakterizujúca pružiny a nazýva sa tuhosť pružiny. Jej jednotka je newton na meter (N/m, čiže N•m-1). Pri meraní silomerom však nič nemusíme počítať, lebo stupnica na ňom je zakreslená priamo v jednotkách sily (newtonoch, kilonewtonoch atď.).
Tiažová sila
Tiažová sila (FG), je sila na Zemi, ktorá vzniká zložením gravitačnej a odstredivej sily. Pôsobí zvislo nadol. Súvisí s hmotnosťou telesa. Vypočítame ju ako súčin hmotnosti telesa a tiažového zrýchlenia.
Tiažové zrýchlenie (g) je fyzikálna veličina, ktorá vyjadruje, akou silou je teleso s hmotnosťou 1kg priťahované k danému telesu (väčšinou vesmírnemu) na danom mieste. Jednotka tiažového zrýchlenia je newton na kilogram (N/kg=N•kg-1). Tiažové zrýchlenie na Zemi v našich zemepisných širkach má hodnotu 9,81N•kg-1. Na rovníku má hodnotu 9,78N•kg-1 a na póloch 9,83N•kg-1. Okrem zemepisnej šírky ho veľmi mierne ovplyvňuje aj nadmorská výška. Pri výpočtoch môžeme pracovať aj zo zaokrúhenou hodnotou tiažového zrýchlenia 10N•kg-1. Jednotku sily 1N si môžeme definovať ako silu, akou Zem priťahuje teleso s hmotnosťou približne 100g (v skutočnosti 101,93679918...).
V niektorých zdrojoch (okrem iných aj učebnica fyziky pre 8.ročník) sa uvádza tiažová sila ako gravitačná a tiažové zrýchlenie ako gravitačné zrýchlenie alebo gravitačná konštanta. ALE NIE JE TO SPRÁVNE, lebo gravitačná sila je len jednou zložkou tiažovej sily (druhou je odstredivá sila) a veličiny gravitačné zrýchlenie a gravitačná konštanta predstavujú niečo úplne iné!
Ťažisko
Ťažisko je bod, ktorý je pôsobiskom tiažovej sily. Teleso zotrváva v pokoji ak ho podoprieme priamo pod ťažiskom alebo zavesíme priamo nad ťažiskom. Každé teleso má práve jedno ťažisko. Poloha ťažiska závisí od rozloženia látky, z ktorej je teleso zložené. Pravidelné telesá majú ťažisko vo svojom strede. Ťažisko môže ležať aj mimo telesa (napríklad prsteň má ťažisko mimo telesa).
Ťažisko plochých nepravidelných telies môžeme určiť metódou ťažníc. Ťažnica je zvislá priamka, ktorá prechádza bodom závesu a ťažiskom. Ťažisko teda určujeme takto:
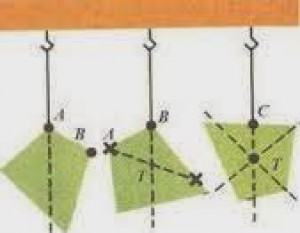Teleso si zavesíme a počkáme, kým sa ustály (zostane v pokoji).- Na rovnakom mieste, kde sme zavesili teleso, zavesíme olovnicu (šnúrku so závažím na konci) a počkáme kým sa ustály (zostane v pokoji). Olovnica po ustálení smeruje zvislo nadol (v smere tiažovej sily).
- Tadiaľ, kadiaľ šnúrka z olovnice prechádza popri telese, nakreslíme priamku. Tá priamka bude totožná s ťažnicou.
- Teleso zavesíme na inom bode a opakujeme postup. Nakreslíme teda ďalšiu ťažnicu.
- Ťažisko leží v priesečníku ťažníc.
Niečo navyše: rovnovážna poloha
Rovnovážna poloha je poloha, v ktorej je teleso v pokoji. Teleso je v rovnovážnej polohe, ak ho zavesíme nad ťažiskom, alebo podoprieme pod ťažiskom.
Podľa vzájomnej polohy ťažiska a vodorovnej osi otáčania rozlišujeme tieto rovnovážne polohy:
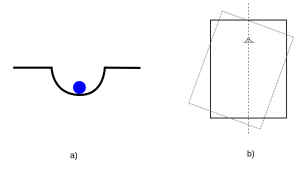Stála (stabilná) rovnovážna poloha - rovnovážna poloha, do ktorej sa teleso po malom vychýlení vráti. Príkladom je teleso nachádzajúce sa v jamke. Po vychýlení sa vráti opäť do najnižšej polohy. Iným príkladom môže byť zavesené teleso, pričom bod závesu sa nachádza nad ťažiskom.
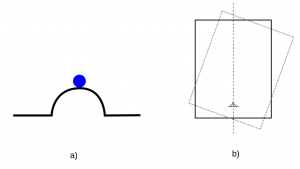Vratká (labilná) rovnovážna poloha - rovnovážna poloha, pri ktorej teleso po malom vychýlení prejde do stálej rovnovážnej polohy. Príkladom môže byť guľôčka na kopčeku. Po vychýlení sa z kopčeka skotúľa. Iným príkladom môže byť zavesené teleso, pričom bod závesu sa nachádza pod ťažiskom.
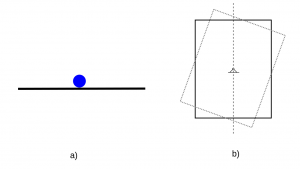Voľná (indiferentná) rovnovážna poloha - rovnovážna poloha, pri ktorej teleso po malom vychýlení ostáva v novej rovnovážnej polohe, ktorá je taktiež voľná. Príkladom môže byť guľôčka na vodorovnej ploche. Po vychýlení zostane v novej polohe. Iným príkladom môže byť zavesené teleso, pričom bod závesu sa nachádza v ťažisku.
Pod malým vychýlením sa tu rozumie nekonečne malé (tzv. infinitezimálne) vychýlenie.
Telesá môžu mať aj viac stálych rovnovážnych polôh, avšak niektoré z nich sú stabilnejšie ako iné, t.j. majú väčšiu stabilitu. Stabilita je schopnosť telesa odolávať prevráteniu. Stabilita je tým väčšia, čím sa ťažisko nachádza nižšie.
Skladanie síl
Skladať sily znamená určiť takú silu (tzv. výslednicu síl), aká má na teleso rovnaký účinok ako sily, ktoré skladáme (zložky). Pri skladaní síl využívame fakt, že vektor (a teda aj ľubovoľná vektorová veličina, ktorou je aj sila) sa nemení, ak ho posúvame po priamke (čiže je to stále rovnaký vektor, ak má rovnakú veľkosť a smer, nezáleží na polohe).
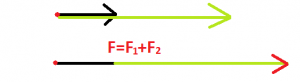Výslednica síl, ktoré pôsobia rovnakým smerom sa rovná súčtu jednotlivých zložiek a jej smer je rovnaký ako smer zložiek.
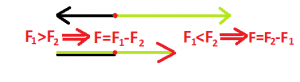Výslednica síl, ktoré pôsobia opačným smerom sa rovná rozdielu jednotlivých zložiek a jej smer je rovnaký ako väčšia sila zo zložiek. Ak sú obe sily rovnaké (rozdiel je 0N), teleso sa nehýbe a správa sa (ak sa neroztrhne:-)), akoby naň nepôsobila žiadna sila. Tejto situácii hovoríme, že sily sú v rovnováhe.
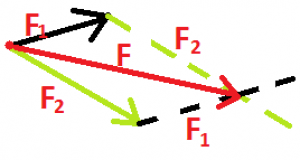Ak sily pôsobia rôznym smerom, výslednicu síl získame doplnením do rovnobežníka síl (čiže nakreslíme si rovnobežku k prvému vektoru, ktorá pretína koniec druhého vektora a rovnobežku k druhému vektoru, ktorá pretína koniec prvého vektora). Výslednica síl má začiatok, samozrejme, v pôsobisku a koniec v opačnom vrchole rovnobežníka. Odmeriame si ju a tak zistíme jej veľkosť, odmeriame si aj uhol medzi ňou a jednou zo zložiek a tak zistíme jej smer. Aj pri silách pôsobiacich rôznym smerom sa dá zistiť smer a veľkosť výslednice síl nielen graficky, ale aj výpočtom, no na základnej škole sa to neučí.
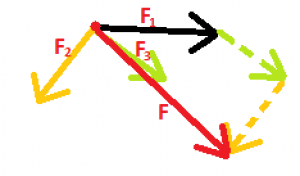Ak skladáme viac ako 2 sily, vektor jednej zo síl si posunieme po priamke tak, aby bol jeho začiatok v bode, kde je koniec iného vektora, k jeho koncu posunieme ďalší vektor atď. Výslednica síl má začiatok, samozrejme, v pôsobisku a koniec na konci posledného vektora.
Rovnako ako sily skladáme všetky vektorové veličiny.
Niečo navyše: výpočet výslednice síl pôsobiacich rôznym smerom
Vyššie som uviedol, že aj pri silách pôsobiacich rôznym smerom sa dá zistiť smer a veľkosť výslednice síl výpočtom. Ale ako sa to robí?
Ak sú jednotlivé sily na seba kolmé, máme pomerne ľahkú prácu, lebo rovnobežník síl bude štvorec (ak sú sily rovnaké) alebo obdĺžnik (ak sú sily rôzne). Výslednica síl ho rozdeľuje na 2 pravouhlé trojuholníky, a tak vieme jednoducho vypočítať výslednicu síl pomocou pytagorovej vety. Výslednica bude vždy zvierať uhol 45° s každou zo zložiek.
|
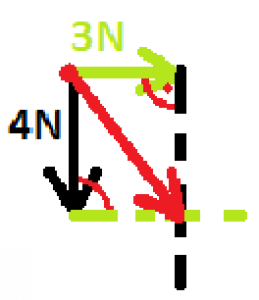
Zadanie: Na bod A pôsobí sila F1 s veľkosťou 3N a sila F2 s veľkosťou 4N. Tieto sily sú na seba kolmé. Akú veľkosť má výslednica týchto síl?
Zápis a obrázok:
Výpočet: α=90° ⇒ F=√(F12+F22) F=√((3N)2+(4N)2)=√25N2=5N F=5N
Odpoveď: Výslednica síl F1 a F2 má veľkosť 5N. |
Ak však sily na seba kolmé nie sú, rovnobežník síl nie je štvorec ani obdĺžnik, a teda výslednica síl ho síce rozdeľuje na zhodné 2 trojuholníky, ale tie nie sú pravouhlé a nepoznáme ani uhly, ktoré zviera výslednica s jednotliými zložkami. Pytagorova veta nám teda veľmi nepomôže, musíme použiť sínusovú vetu (a/sinα=b/sinβ=c/sinγ) a vylepšenú pytagorovu vetu, tzv. kosínusovú vetu (c2=a2+b2-2•a•b•cosγ), ktorá platí v každom trojuholníku, nielen v pravouhlom.
|
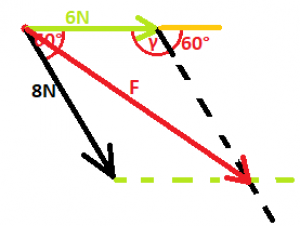
Zadanie: Na bod A pôsobí sila F1 s veľkosťou 6N a sila F2 s veľkosťou 8N. Tieto sily zvierajú uhol 60°. Akú veľkosť má výslednica týchto síl a aký uhol zviera so silou F1?
Zápis a obrázok:
Výpočet: Najprv si vypočítame uhol γ, t. j. uhol na vrcholoch rovnobežníka, ktoré sú susedné (nie protiľahlý) vrcholy k pôsobisku síl F1 a F2. Vieme, že uhol, ktorý je mu susedný, je súhlasný s uhlom, ktorý zvierajú sily F1 a F2, a teda má rovnakú veľkosť (pozri uhly, rovnobežky preťaté priamkou), čiže 60°. Súčet susedných uhlov musí byť 180°, a teda uhol γ si vypočítame ako rozdiel 180° a 60°. γ=180°-α = 180°-60°=120°
Teraz pomocou kosínusovej vety vypočítame veľkosť výslednice síl. F=√(F12+F22-2•F1•F2•cosγ) F=√((6N)2+(8N)2-2•6N•8N•cos(120°)) F≈12,17N
Pomocou sínusovej vety si odvodíme vzorec na výpočet sínusu uhla medzi výslednicou síl a silou F1. Pomocou tohto vzorca si sínus tohto uhla vypočítame. F/sinγ=F1/sinβ /•sinβ•sinγ F•sinβ=F1•sinγ /:F sinβ=F1•sinγ/F sinβ=6
Nakoniec si vypočítame uhol β pomocou sínusu uhla β. Na výpočet uhla z jeho sínusu nám slúži operácia sínus na mínus prvú (sin-1), respektíve arkussínus (arcsin). β=arcsin(sinβ)=arcsin(0,4296)=25,44°
Odpoveď: Výslednica síl F1 a F2 má veľkosť 12,17N a so silou F1 zviera uhol 25,44°. |
Niečo navyše: rozklad sily
Sily sa dokážu nielen skladať, ale aj rozkladať. Rozložiť silu na zložky znamená nájsť dve alebo viac takých síl, ktorých výslednica sa rovná danej sile. Niekedy sa sila môže rozložiť aj na zložky väčšie, ako je ona sama.
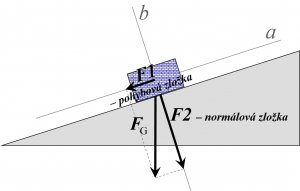Napríklad tiažová sila pôsobiaca na teleso šmýkajúce sa po šikmej ploche sa rozloží na normálovú zložku (ktorá je kolmá na plochu) a pohybovú zložku (ktorá smeruje nadol, je rovnobežná s rovinou a spôsobuje pohyb telesa). Uhol, ktorý zviera normálová zložka sily s pôvodnou silou bude rovnaký, ako zviera daná naklonená rovina s vodorovnou rovinou (vyplýva to zo zhodnosti a podobnosti trojuholníkov).
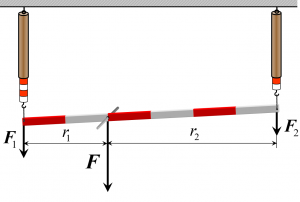Ak silu rozkladáme na 2 rovnobežné zložky, tak platí:
- Súčet veľkostí zložiek sa rovná veľkosti rozkladanej sily (F=F1+F2).
- Pomer vzdialeností vektorových priamok (t.j. priamok, ktorých časťou je celý vektor, ktorým znázorňujeme danú silu) zložiek sa rovná prevrátenému pomeru veľkosti zložiek (F1/F2=r2/r1).
|
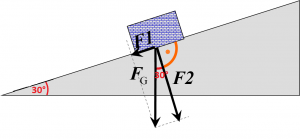
Zadanie: Na teleso šmýkajúce sa po naklonenej rovine pôsobí tiažová sila 200N. Naklonená rovina zviera s vodorovnou rovinou uhol 30°. Akú veľkosť budú mať zložky, na ktoré sa tiažová sila rozloží?
Zápis a obrázok:
Výpočet: Tiažová sila a jej zložky tvoria spolu pravouhlý trojuholník, kde je tiažová sila preponou, pohybová zložka (F1) protiľahlou odvesnou k uhlu α (30°) a normálová zložka (F2) priľahlou odvesnou k uhlu α (30°).
Keďže protiľahlá odvesna ku prepone predstavuje goniometrickú funkciu sínus, pohybovú zložku (protiľahlú odvesnu) vypočítame vynásobením sínusu uhla α tiažovou silou (preponou). F1=FG•sin(α)=200N•sin(30°)=200N•0,5=100N
A keďže priľahlá odvesna ku prepone predstavuje goniometrickú funkciu kosínus, normálovú zložku (priľahlú odvesnu) vypočítame vynásobením kosínusu uhla α tiažovou silou (preponou). F2=FG•cos(α)=200N•cos(30°)≈173,2N
Odpoveď: Pohybová zložka F1 má veľkosť 100N a normálová zložka F2 má veľkosť 173,2N. |
|
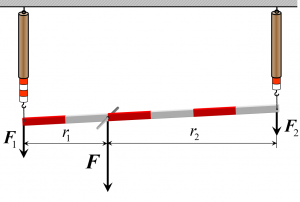
Zadanie: Na teleso zavesené na tyči so zanedbateľnou hmotnosťou pôsobí tiažová sila 6N. Tyč je zavesená za svoje konce na silomeroch. Vzdialenosť telesa od prvého silomeru je 0,2m a od druhého silomeru 0,4N. Aké veľkosti síl budú ukazovať silomery?
Zápis a obrázok:
Výpočet: Z vyššie uvedených zákonitostí si pomocou rovnice odvodíme vzorec na výpočet zložky F1 a pomocou tohto vzorca si zložku F1 aj vypočítame. F2 bude v rovnici vyjadrená ako FG-F1. F1/FG-F1=r2/r1 /•r1•(FG-F1) F1•r1=r2•FG-r2•F1 /+r2•F1 F1•r1+F1•r2=FG•r2 F1•(r1+r2)=FG•r2 /:(r1+r2) F1=FG•r2/r1+r2 F1=6N•0,4m/0,2m+0,4m=2,4N•
Keďže pri rozklade sily na rovnobežné zložky sa súčet všetkých zložiek musí rovnať rozkladanej sile, tak zložka F2 sa musí rovnať rozdielu tiažovej sily a zložky F1. F2=FG-F1=6N-4N=2N
Odpoveď: Prvý silomer (ktorý je od závažia vzdialený 0,2m) bude ukazovať 4N a druhý silomer (ktorý je od závažia vzdialený 0,4m) bude ukazovať 2N. |
Otáčavé účinky sily
Pohybové účinky sily môžu byť posuvné alebo otáčavé. otáčavé účinky sily meriame pomocou vektorovej fyzikálnej veličiny moment (otáčavý účinok) sily (M). Moment sily vypočítame ako súčin veľkosti sily a ramena sily (M=F•r). Rameno sily je kolmá vzdialenosť vektorovej priamky (t. j. priamky, ktorej časťou je celý vektor, ktorým znázorňujeme danú silu) od osi otáčania. Keďže jednotkou sily je newton a jednotkou ramena sily (keďže je to vlastne vzdialenosť, čiže dĺžka) je meter, jednotkou momentu sily bude newtonmeter (Nm). Ak na teleso otáčané okolo nehybnej osi pôsobí súčasne viacero síl, výsledný moment sily sa rovná súčtu ich momentov síl.
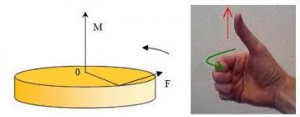Smer momentu sily určíme podľa pravidla pravej ruky: ak otáčané teleso teleso chytíme pravou tak, že prsty ukazujú smer otáčania, tak palec ukazuje smer momentu sily. Moment sily je kladný, ak smeruje k nám a záporný, ak smeruje od nás. Z toho vyplýva, že teleso sa otáča v kladnom smere (zmysle), ak sa otáča proti smeru hodinových ručičiek a v zápornom smere (zmysle), ak sa otáča v smere hodinových ručičiek. Smer a znamienko momentu sily, rovnako ako to, ktorým smerom sa teleso otáča, sú relatívne, keďže to závisí od toho, z ktorej strany sa na teleso pozeráme.
Páka je tyč otáčavá okolo pevnej osi otáčania. Páka môže byť jednoramenná (končí sa na osi otáčania, napríklad francúzsky kľúč) alebo dvojramenná (pokračuje aj za osou otáčania, napríklad hojdačka). Vďaka dlhému ramenu nám pri použití páky v praxi stačí malá sila na prekonanie veľkej sily. V praxi páku využívame napríklad v luskáčiku na orechy, otvaráku fľaše, pri dvíhaní fúrika alebo pri uvoľňovaní matíc pomocou kľúča.
|
Zadanie: Na uvoľnenie matice je potrebný moment sily 5Nm. Akou veľkou silou musíme pôsobiť, ak použijeme kľúč dlhý 10 cm?
Zápis:
Výpočet: M=F•r ⇒ F=M/r F=5Nm/0,1=50N
Odpoveď: Musíme pôsobiť silou 50N. |
|
Zadanie: Deti Marcel a Martin sa išli hojdať na hojdačke. Marcel je však tučný a váži 58kg, zato Martin je chudý a váži len 32kg. Martin si sadol na koniec hojdačky, ktorý je od jej osi otáčania vzdialený 2m. Do akej vzdialenosti si má sadnúť Marcel, ak chlapci chcú, aby hojdačka bola vyrovnaná?
Zápis: g=9,81Nkg-1≈10Nkg-1 m(Martin)=32kg r(Martin)=2m M(Martin)=M(Marcel) m(Marcel)=58kg FG(Martin)=? FG(Marcel)=? r(Marcel)=?
Výpočet: Aby bola vyrovnaná hojdačka, musia byť vyrovnané momenty tiažových síl Martina a Marcela. Najprv si teda vypočítame moment sily pomocou údajov o Martinovi. Budeme rátať zo zaokrúhlenou hodnotou tiažového zrýchlenia (10Nkg-1). M=r(Martin)•FG(Martin)=r(Martin)•m(Martin)•g M=2m•32
Teraz si vypočítame tiažovú silu Marcela. Budeme rátať so zaokrúhlenou hodnotou tiažového zrýchlenia (10Nkg-1). FG(Marcel)=m(Marcel)•g FG(Marcel)=58
Nakoniec, keď vydelíme moment sily tiažovou silou Marcela, získame výsledné rameno sily, čiže vzdialenosť od osi otáčania hojdačky do ktorej si Marcel má sadnúť. r(Marcel)=M/FG(Marcel)=640
Druhá (a podľa mňa jednoduchšia) možnosť výpočtu je pomocou trojčlenky, keďže pri rovnakom momente sily platí medzi silou a jej ramenom nepriama úmernosť. ⇩32kg............................2m⇧ ⇩58kg...............................x⇧ r(Marcel)=x=32
Odpoveď: Marcel si má sadnúť do vzdialenosti 1,1m od osi otáčania hojdačky. |
Trenie
Trenie je jav, ktorý vzniká medzi dvomi vzájomne sa dotýkajúcimi telesami a brzdí ich vzájomný pohyb. Príčinou trenia je skutočnosť, že dotykové plochy telies nie sú nikdy dokonale hladké a ich nerovnosti do seba zapadajú. Ďalšou príčinou trenia je vzájomné priťahovanie častíc telies. Plochy sa trením mechanicky vyhladzujú. Pri trení vzniká trecia sila, ktorá pôsobí proti pohybu telesa. Veľkosť trecej sily závisí od normálovej sily pôsobiacej na podložku a drsnosti povrchu.
Existuje pokojové aj pohybové trenie. Pokojové trenie má väčšiu treciu silu ako pohybové trenie. Čiže na uvedenie telesa do pohybu je potrebná väčšia sila ako na udržanie ho v pohybe.
Trenie môže byť škodlivé aj užitočné. Škodlivé trenie je napríklad v strojných zariadeniach. Snažíme sa ho zmenšiť napríklad rôznymi mazivami alebo použitím ložísk. Užitočné trenie napríklad pomáha pri brzdení. Vieme ho zväčšiť pritlačením na povrch (napríklad keď brzdíme pri lyžovaní, tak pritláčame nohy k snehu) alebo zdrsnením povrchu (napríklad v zime posýpame cesty a vymieňame pneumatiky za pneumatiky s väčším dezénom, ktoré majú väčšie drážky, čiže drsnejší povrch).
Niečo navyše: šmykové a valivé trenie
Trenie sa delí na šmykové a valivé.
Šmykové trenie vzniká, keď sa teleso šmýka po povrchu. Treciu silu pri šmykovom trení vypočítame ako súčin normálovej sily a koeficientu šmykového trenia medzi danými povrchmi (Ft=f•Fn). Koeficient šmykového trenia (f) je bezrozmerná veličina a možno ju nájsť v tabuľkách pre rôzne kombinácie povrchov. Pre každú kombináciu možno nájsť 2 rôzne hodnoty: pre pokojové trenie (f0) a pohybové trenie (f).
Valivé trenie vzniká, keď sa teleso valí po kolesách alebo valčekoch. Okrem normálovej sily a drsnosti povrchu závisí ešte od polomeru kolies alebo valčekov. Treciu silu pri šmykovom trení vypočítame ako súčin koeficientu valivého trenia a podielu normálovej sily a polomeru valčekov (Ft=ξ•Fn/r). Koeficient valivého trenia (ξ -ksí) má jednotku meter a možno ho nájsť v tabuľkách pre rôzne kombinácie povrchov.