Mechanika: práca, výkon a energia
Práca (fyzikálna práca, mechanická práca)
Z fyzikálneho hľadiska konáme prácu (W), ak pôsobíme na teleso silou, ktorá spôsobí jeho pohyb. Práca je fyzikálna veličina so značkou W (z anglického work) a jednotkou rovnakou ako teplo, čiže joule (J, čítaj ,,džaul"). Prácu vypočítame ako súčin sily pôsobiacej na teleso v smere pohybu a dráhy, ktorú prejde. Vzorec na výpočet práce teda je w=F•s, takže práca 1J vzniká pri pôsobení silou 1N po dráhe 1m (J=N•m). Zo vzorca si vieme odvodiť vzorce na výpočet dráhy (s=w/F) a sily (F=w/s). Sila kolmá na smer pohybu (resp. sila, ktorá nevyvoláva pohyb) prácu nekoná (čiže keď držíme nejaký predmet a nepohybujeme s ním, z fyzikálneho hľadiska nekonáme prácu, aj keď sa namáhame, aby sme ho udržali). Ak sa sila rozloží (čiže smer pohybu zviera so silou nejaký uhol), prácu koná len jej pohybová zložka. Ak sila pôsobí proti pohybu (príkladom takejto sily je trecia sila), musíme vynaložiť väčšiu silu, a teda aj väčšiu prácu na pohyb telesa. Hovoríme teda, že sila pôsobiaca proti pohybu prácu spotrebúva.
Vyrieš príklady (riešenia sú na konci príspevku):
1.) Akú prácu vykoná chlapec s hmotnosťou 52kg, ktorý má na chrbte batoh s hmotnosťou 1,5kg, keď rovnomerným pohybom po zvislom rebríku vystúpi do výšky 10m?
2.) Žeriav dvíha náklad rovnomerným pohybom do výšky 20m, pričom vynaloží prácu 115kJ. Akú hmotnosť má náklad?
Práca na naklonenej rovine a na kladke
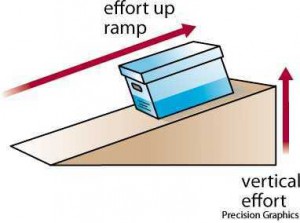Naklonená rovina (obrázok vľavo) je rovina ktorá zviera s horizontálnym (vodorovným) povrchom uhol, ktorý je iný ako pravý. Umožňuje nám prekonať veľký odpor (napríklad pri dvíhaní ťažkých telies), pričom je potrebné vynaložiť relatívne malú silu. Čím dlhšiu naklonenú rovinu použijeme, tým menšiu silu potrebujeme vynaložiť. Avšak naklonená rovina prácu nešetrí, lebo hoci zmenšuje potrebnú silu, rovnako zväčšuje dráhu.
 |
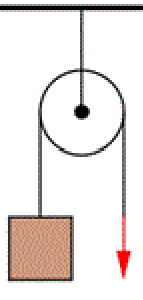Pevná kladka (obrázok vľavo) je jednoduchý stroj skladajúci sa z upevneného kolesa otáčajúceho sa okolo vlastnej osi, ktoré má po obvode drážku v ktorej sa pohybuje lano, ktorého oba konce smerujú nadol. Na jednom z nich je náklad a druhý koniec ťaháme. Prácu nešetrí, nemení ani dráhu, ani potrebnú silu. Mení len smer pôsobiacej sily, keďže sa nám lepšie ťahá nadol ako nahor. |
 |
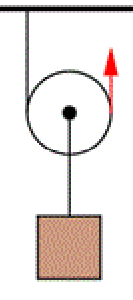Voľná kladka (obrázok vľavo) je jednoduchý stoj skladajúci sa z kolesa upevneného na náklad, ktoré má po obvode drážku v ktorej sa pohybuje lano, ktorého oba konce smerujú nahor, pričom jeden koniec je hore pevne zachytený. Takáto jednoduchá voľná kladka zmenšuje silu potrebnú na dvíhanie nákladu o polovicu. Avšak ani voľná kladka prácu nešetrí, lebo hoci potrebnú silu o dvojnásobne zmenšuje, dráhu dvojnásobne zväčšuje. |
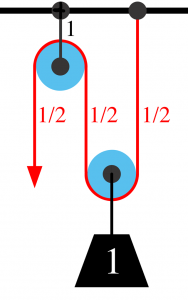Pri voľnej kladke máme taký problém, že musíme ťahať nahor, pričom by sa nám lepšie ťahalo nadol. Preto väčšinou využívame kombináciu pevnej a voľnej kladky - kladkostroj. Jednoduchý kladkostroj je zobrazený na obrázku vľavo. Kladkostroj alebo voľná kladka však nemusia byť len také jednoduché. Môžu sa skladať aj z viacerých kladiek. 
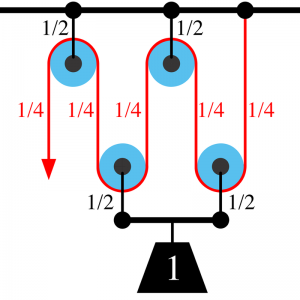Čím viac voľných kladiek zložená kladka obsahuje, tým viac zmenšuje potrebnú silu a zväčšuje dráhu (dve voľné kladky zmenšujú silu na tretinu a dráhu strojnásobujú, tri zmenšujú silu na štvrtinu a dráhu zväčšujú štvornásobne...). Na obrázku vpravo je zobrazený kladkostroj , ktorý sa skladá z troch voľných kladiek (silu teda zmenšuje na štvrtinu a dráhu zväčšuje štvornásobne) a jednej pevnej kladky (aj keď kladka vpravo hore môže vyzerať ako pevná, v skutočnosti je voľná).
Vyrieš príklad (riešenia sú na konci príspevku):
3.) Teleso s hmotnosťou 25kg potrebujeme dostať do výšky 7m. Akú silu musíme vynaložiť ak ho kotúľame rovnomerným pohybom a použijeme naklonenú rovinu so sklonom 30%? (Poznámka: sklon 30% znamená, že na každých 100m dĺžky vo vodorovnom smere prekonáme stúpanie 30m.)
Výkon
1 žeriav zdvihne náklad za 5 sekúnd a druhý ho zdvihne za 10 sekúnd. Ktorý z nich vykoná väčšiu prácu? Ani jeden, oba vykonajú prácu rovnakú. Ale prvý má väčší výkon, lebo vykoná rovnakú prácu za kratší čas.
Výkon (P) je fyzikálna veličina, ktorá udáva množstvo práce vykonanej za určitý čas. Jej značka je P (z anglického ,,power") a jednotka Watt (W). Vypočítame ju tak, že prácu vydelíme časom, za ktorý bola vykonaná. Vzorec na výpočet výkonu teda je P=W/t, takže výkon 1 watt zodpovedá práci 1 Joule vykonanej za jednu sekundu (W=J/s).
Vyrieš úlohy (správne riešenia sú na konci príspevku):
4.) Cyklista vychádza na kopec stálou rýchlosťou. Dĺžka kľuky pedála je 25 centimetrov, jedna otočka pedála trvá 2 sekundy, priemerná sila na pedál má veľkosť 150N. Určte priemerný výkon cyklistu.
5.) Pásový dopravník s výkonom 15kW dvíha cukrovú repu do výšky 2m. Aká je hmotnosť cukrovej repy naloženej za 5 minút?
Energia
Keď do luku vložíme šíp, potom jeho tetivu natiahneme (tým sa namáhame - konáme prácu) a pustíme, tak tetiva sa prudko vráti do pôvodnej polohy a šíp vystrelí. Natiahnutím tetivy (konaním práce) sme spôsobili, že tetiva bola schopná po pustení tiež konať prácu (vystreliť). Inými slovami - natiahnutím sme tetive dodali energiu (,,uloženú" prácu).
Energia (E) je schopnosť telesa (alebo sústavy) konať prácu, čiže akási ,,uložená" práca. Energiu teleso (sústava) získava konaním práce. Jej hodnota sa teda rovná práci, ktorú je teleso schopné vykonať, ale ešte nevykonalo. Inak povedané, kým práca je dej (proces), energia je stav. Je to fyzikálna veličina so značkou E a jednotkou rovnakou ako práca - Joule (J). Energia môže byť uložená v telese (sústave) v rôznych formách. Podľa toho rozlišujeme energiu mechanickú, akustickú, žiarivú, tepelnú, chemickú, jadrovú, elektrickú a magnetickú.
Mechanická energia (polohová a pohybová)
Mechanickú energiu môžeme rozdeliť na dva druhy: polohovú (potenciálnu) energiu (Ep) a pohybovú (kinetickú) energiu (Ek).
Polohová energia závisí od polohy telesa a rovná sa práci, ktorá sa pri zmene polohy telesa spotrebovala a ktorú môže teleso pri návrate do pôvodnej polohy vykonať. Podľa sily, ktorá prácu spotrebúva rozlišujeme potenciálnu energiu tiažovú, pružnosti, magnetickú, elektrickú...
Polohovú energiu tiažovú vypočítame ako súčin tiažovej sily pôsobiacej na teleso a výšky telesa nad podložkou - nulovou hladinou (Ep=FG•h=m•g•h). Je relatívna, závisí od toho, kde si určíme nulovú hladinu (napríklad kniha s hmotnosťou približne 500g nachádzajúca sa vo výške 1m nad stolom, ktorý je vysoký 80cm, má polohovú energiu približne 5J vzhľadom na dosku stola a približne 9J vzhľadom na zemský povrch). Polohová energia môže byť aj záporná (napríklad polohová energia vedra v studni vzhľadom na zemský povrch).
Polohovú energiu pružnosti majú deformované pružné telesá. Pri návrate do pôvodného tvaru vykonajú rovnakú prácu, aká je potrebná na ich deformáciu.
Pohybová energia je energia, ktorú majú pohybujúce sa telesá. Závisí od hmotnosti a rýchlosti (keď po vás niečo hodím, tým viac náraz pocítite, čím ťažšie bude teleso a čím väčšiu rýchlosť bude mať). Jej hodnota sa rovná práci, ktorú je potrebné vykonať na to, aby sme daný objekt uviedli z pokoja do rovnomerného pohybu s danou rýchlosťou. Na základe toho si vieme odvodiť vzorec na výpočet pohybovej energie: vzorec pre prácu je F•s. Za silu si dosadíme vzorec na jej výpočet podľa 2. newtonovho pohybového zákona (F=m•a) a za dráhu vzorec pre výpočet dráhy rovnomerne zrýchleného pohybu s nulovou počiatočnou rýchlosťou (s=1/2•a•t2). Dostaneme teda vzorec m•a•1/2•a•t2, ktorý si upravíme do tvaru 1/2•m•(a•t)2. Za zrýchlenie si vieme dosadiť vzorec na jeho výpočet (a=Δv/t) v ktorom si môžeme zmenu rýchlosti nahradiť rýchlosťou, keďže počiatočná rýchlosť je nulová. Dostaneme teda vzorec Ek=1/2•m•(v/t•t)2, v ktorom sa nám však čas vykráti a ostane iba Ek=1/2•m•v2.
Polohová a pohybová energia sa navzájom na seba menia. Napríklad padajúce teleso má na začiatku pádu svoju maximálnu polohovú energiu, ktorá sa postupne, ako padá, mení na pohybovú. Pri dopade má maximálnu pohybovú energiu a nulovú polohovú energiu (v skutočnosti to takto ideálne nefunguje, lebo energia sa aj stráca - napríklad vďaka odporu vzduchu sa mení na tepelnú). Takto sa energia premieňa aj pri chodení, šmýkaní a kotúľaní z kopca do doliny a opačne, skákaní na trampolíne a v mnohých ďalších situáciách. Zákon zachovania energie hovorí, že energia sa nedá vyrobiť ani zničiť, len mení svoje formy.
Vyrieš príklady (riešenia sú na konci príspevku):
6.) Akú veľkú potenciálnu energiu má 5m3 vody z priehrady, ktorá pri stekaní dole a poháňaní turbíny klesne o 50 metrov?
Energia v prírode
Takmer všetka energia na Zemi aj v našom organizme pochádza zo slnka. Slnko ohrieva na určitých miestach vzduch, mení sa tlak, atmosféra teda nikdy nie je v rovnováhe, do ktorej sa však snaží dostať, teplý vzduch stúpa a studený klesá. V dôsledku toho všetkého vzniká vietor - pohybujúci sa vzduch s kinetickou energiou, ktorý využívame napríklad pri výrobe elektriny vo veterných elektrárňach. Slnko ohrieva vodnú hladinu, čo spôsobuje vyparovanie vody, vodná para potom stúpa nahor, v atmosfére ochladne a klesne vo forme dažďa, snehu alebo krúpov. Dažde naplnia potoky a rieky, ktoré majú pri toku pohybovú energiu. V priehradách ju premeníme na polohovú a potom (pri stekaní z priehradného múra) naspäť na pohybovú a následne na elektrickú. Slnečnú energiu využívajú aj rastliny, ktoré ju menia fotosyntézou na chemickú. Zvieratá a ľudia, keď rastliny zjedia, ju využívajú a menia na tepelnú a pohybovú, niektorú si ukladajú v tele vo forme chemickej energie. Uhlie, ropa a zemný plyn majú v sebe veľa chemickej energie, ktorá taktiež pochádza zo slnka. Vznikli totiž zo zvyškov rastlín a živočíchov (živočíchy získali chemickú energiu z rastlín alebo ďalších živočíchov a rastliny fotosyntézou zo slnka).
Energia je pre človeka užitočná, ale dokáže byť aj nebezpečná. Kvôli energii v našej zemi vybuchujú sopky, vznikajú zemetrasenia vlny tsunami. Neopatrná manipulácia s energiou je nebezpečná (veď aká katastrofa sa stala v jadrovej elektrárni v Černobyle). Ľudia takisto energiu zneužívajú (zbrane, bomby...). Mali by sme si dávať pozor aj na plytvanie energiou. Fosílne palivá môžeme veľmi rýchlo minúť. Ich využívanie takisto spôsobuje znečisťovanie ovzdušia a globálne otepľovanie. Žiaden spôsob výroby elektrickej energie nie je úplne ekologický. Napríklad aj vodné elektrárne škodia rybám, veterné vtákom, slnečné zaberajú pôdu, kde by mohli rásť rastliny... Najlepší spôsob ako s akoukoľvek energiou narábať ekologicky, je neplytvať ňou.
Niečo navyše
Trochu iné jednotky
Možno ste si všimli, že elektrická energia (a elektrická práca) je na vašom elektromery meraná nie v jouloch, ale v iných jednotkách - kilowatthodinách (kWh). Aký je prevod joulu na kilowatthodinu a opačne? Keďže prácu vypočítame vynásobením výkonu časom, tak jeden joule bude vlastne jedna wattsekunda. W premeníme na kW vydelením 1000 a sekundu na hodinu vydelením 3600 (60•60). Čiže J premeníme na kWh vydelením 3600000 (1000•3600). Pri opačnej premene, čiže kilowatthodín na jouly budeme naopak násobiť. Čiže: kWh=3600000•J a J=1/3600000•kWh. Môžeme si zapamätať aj že kWh=3,6•MJ a MJ=1/3,6•kWh.
Aj výkon vieme určiť v iných jednotkách, ako sú jednotky sústavy SI. V automobiloch sa dodnes výkon udáva nie vo wattoch ale v inej jednotke (ktorú mimochodom vymyslel James Watt
) - kôň (resp. konská sila). Táto jednotka má rôzne značky: slovenská k, staršie ks alebo KS; anglická (používaná však aj v iných krajinách a niekedy aj na Slovensku) HP alebo hp (z horse power), francúzska ch (z cheval-vapeur), nemecká PS (z Pferdestärke)... Rovnako ako má jednotka rôzne značky, tak má aj rôzne hodnoty (ktoré sa menili aj počas histórie). Dnes sa najčastejšie používajú dve hodnoty: Jednou je metrický (kontinentálny, európsky) kôň (735,5W, presnejšie 735,49875W) používaný v kontinentálnej Európe, Ázii a Južnej amerike. Druhou je mechanický (anglický, americký, imperiálny) kôň (745,7J, presnejšie 745,69987158227022J) používaný vo anglicky hovoriacich krajinách a bývalých britských kolóniách.
Príkon a účinnosť
Stroje nevedia využiť všetku energiu (všetok výkon), ktorý im dodáme, lebo časť energie sa stratí. Dodaný výkon (energia dodaná za určitý čas) sa nazýva príkon (P'). Je to fyzikálna veličina so značkou P' a jednotkou rovnakou ako výkon, Watt (W). Čím menší je rozdiel medzi príkonom a výkonom daného zariadenia, tým lepšie. Existuje aj fyzikálna veličina účinnosť, ktorej značka je grécke písmeno η (eta). Táto veličina je bezrozmerná, čo znamená, že nemá jednotku. Vypočítame ju tak, že výkon vydelíme príkonom. Väčšinou ju vyjadrujeme v percentách. Žiadne zariadenie nemá účinnosť, ktorá by dosiahla 100%, lebo vždy sa nejaká energia stratí.
|
1.) Zadanie: Akú prácu vykoná chlapec s hmotnosťou 52kg, ktorý má na chrbte batoh s hmotnosťou 1,5kg, keď rovnomerným pohybom po zvislom rebríku vystúpi do výšky 10m?
Výpočet: W=FG•h=m•g•h=(m1+m2)•g•h=(52+1,5)
Odpoveď: Chlapec vykoná prácu 5,248kJ. |
|
2.) Zadanie: Žeriav dvíha náklad rovnomerným pohybom do výšky 20m, pričom vynaloží prácu 115kJ. Akú hmotnosť má náklad?
Výpočet: m=FG/g=W/h•g=115000
Odpoveď: Náklad má hmotnosť 586,14kg. |
|
3.) Zadanie: Teleso s hmotnosťou 25kg potrebujeme dostať do výšky 7m. Akú silu musíme vynaložiť ak ho kotúľame rovnomerným pohybom a použijeme naklonenú rovinu so sklonom 30%? (Poznámka: sklon 30% znamená, že na každých 100m dĺžky vo vodorovnom smere prekonáme stúpanie 30m.)
Výpočet: Najprv si vypočítame potrebnú prácu: W=FG•h=m•g•h=25
Potom si vypočítame dĺžku naklonenej roviny, t.j. dráhu, ktorú teleso prejde (Vieme, že stúpanie je 30%, a tak si pomocou trojčlenky vypočítame, koľko to bude pri 7m. Následne pomocou pytagorovej vety dĺžku naklonenej roviny): ⇧30m........................100m⇧ ⇧7m.................................x⇧ x=7 s=√((23,3333m)2+(7m)2)≈24,3607
Prácu následne vydelíme dráhou, aby sme zistili potrebnú silu: F=W/h=1716,75
Odpoveď: Musíme vynaložiť silu 70,47N. |
|
4.) Zadanie: Cyklista vychádza na kopec stálou rýchlosťou. Dĺžka kľuky pedála je 25 centimetrov, jedna otočka pedála trvá 2 sekundy, priemerná sila na pedál má veľkosť 150N. Určte priemerný výkon cyklistu zaokrúhlený na celé Watty.
Výpočet: Najprv si vypočítame prejdenú dráhu. Vieme, že cyklista točí pedálmi, čiže dráha má tvar kružnice, ktorje polomerom je kľuka pedála. s=2πr=2•π•0,25m≈1,5708m
Potom si vypočítame výkon cyklistu: P=W/t=F•s/t=150N•1,5708m/2s=117,81W≈118W
Odpoveď: Priemerný výkon cyklistu je 118W. |
|
5.) Zadanie: Pásový dopravník s výkonom 15kW dvíha cukrovú repu do výšky 2m. Aká je hmotnosť cukrovej repy naloženej za 5 minút? Výsledok vyjadrite zaokrúhlený na celé tony.
Zápis: Tiažové zrýchlenie (g).........................................9,81N•kg-1 Výkon dopravníka (P).........................................15kw=15000W Čas (t).................................................................5min=300s Dráha (s).............................................................2m Hmotnosť repy (m)..............................................?
Výpočet: m=F/g=W/s•g=P•t/s•g=15000
Odpoveď: Hmotnosť cukrovej repy naloženej za 5 minút je 229 ton. |
|
6.) Zadanie: Akú veľkú potenciálnu energiu má 5m3 vody z priehrady, ktorá pri stekaní dole a poháňaní turbíny klesne o 50 metrov? Hustota vody je 1000kg•m-3.
Zápis:
Výpočet: Ep=FG•h=m•g•h=ρ•V•g•h Ep=1000
Odpoveď: Voda z priehrady má potenciálnu energiu 24,525MJ. |
(Späť k príkladom sa dostanete kliknutím na číslo príslušného príkladu.)