Elektrický prúd, napätie a odpor

20. 8. 2020

Elektrický prúd

V predchádzajúcom príspevku ste sa dozvedeli, že látky rozdeľujeme na vodiče a izolanty a že vodiče obsahujú voľné častice s nábojom. Budeme sa baviť hlavne o kovoch, takže tu budem hovoriť o elektrónoch, aj keď väčšina zákonitostí, ktoré platia pre elektróny, platí aj pre ostatné voľné častice s nábojom (katióny a anióny).

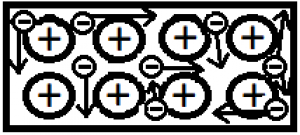
Kým je vodič (kovový drôt) mimo elektrického poľa, elektróny v ňom sa pohybujú náhodnými smermi vďaka tepelnej energii - konajú tzv. tepelný pohyb. Keď drôt zapojíme do zdroja elektrickej energie (t.j. na jeden koniec budeme pôsobiť trvalým kladným nábojom a na druhý koniec trvalým záporným), elektróny sa pôsobením elektrického poľa začnú všetky pohybovať jedným smerom - vytvorili sme uzavretý elektrický obvod, ktorým preteká elektrický prúd.


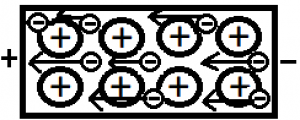Tepelný pohyb v nezapojenom vodiči	Usmernený pohyb v zapojenom vodiči

Elektrický prúd je teda usmernený pohyb voľných častíc s nábojom (v kovoch sú tými časticami elektróny). Vodičom bude pretekať, len ak budeme elektrickým poľom pôsobiť na oba konce drôtu (na jednom konci kladným a na druhom záporným poľom) - t.j. nestačí pôsobiť len na jeden koniec. Dohodnutý smer elektrického prúdu je smer pohybu kladnej častice, čiže od kladného pólu k zápornému (kladný pól kladnú časticu odpudzuje a záporný pól ju priťahuje). Ale keďže v kovoch sú voľnými časticami s nábojom záporné elektróny, tak smer ich pohybu je opačný ako dohodnutý smer prúdu, čiže od záporného pólu ku kladnému (kladný pól zápornú časticu priťahuje a záporný pól ju odpudzuje). Čo znamená, že dohodnutý smer prúdu? Keď sa ešte nevedelo, čo vlastne elektrický prúd spôsobuje, nevedelo sa ani, ako určiť jeho smer. A tak sa dohodlo, že budeme rozmýšľať tak, akoby prúd tiekol od kladného pólu k zápornému. Keď sa zistila podstata prúdu zistilo sa aj to, že v kovových vodičoch tečú záporné elektróny elektróny, a teda že ich smer je opačný ako dohodnutý smer prúdu, bolo rozhodnuté, že od tejto dohody neupustíme, keďže sa na nej už stavalo (napríklad pri schémach elektrických obvodov alebo pri tzv. ampérovom pravidle pravej ruky).

Elektrický prúd je však aj fyzikálna veličina so značkou I a jednotkou ampér (A). Okrem ampéru používame aj jednotky kiloampér (kA) a miliampér (mA). Prierezom vodiča prechádza prúd 1A, ak ním za jednú sekundu prejdú voľné častice s celkovým nábojom 1C.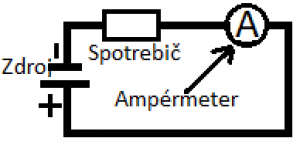
Prúd meriame ampérmetrom. Keďže je definovaný na priereze (čiže vlastne na určitom mieste) vodiča, tak aj ampérmetrom ho musíme merať na priereze vodiča, a preto ampérmeter zapájame do priamo obvodu, tzv. sériovo (za sebou), ako je na obrázku vpravo hore.

Elektrický prúd má rôzne účinky. V tuhých vodičoch spôsobuje ich zohriatie a vytvára okolo nich magnetické pole, v kvapalinách mení ich zloženie (spôsobuje chemické reakcie) a v plynoch spôsobuje svetelné a zvukové efekty.

Aby vodičom trvale prechádzal elektrický prúd, musí byť pripojený na zdroj elektrického napätia (elektrický zdroj), ktorý v ňom udržiava elektrické pole. Elektrický zdroj premieňa nejakú neelektrickú silu na elektrickú silu. Podľa neelektrickej sily, ktorú zdroj premieňa, delíme zdroje na: chemické (galvanické články a akumulátory - klasické ,,baterky"), svetelné (fotočlánky), tepelné-termoelektrické (termočlánky), mechanické (vytvárajú elektrickú silu pomocou trenia, napríklad Van der Graaffov generátor) a elektrodynamické (premieňajú mechanickú silu na elektrickú pomocou magnetickej sily, napríklad dynamo alebo alternátor).

Jednosmerný a striedavý prúd

Poznáme dva druhy elektrického prúdu: jednosmerný a striedavý. Aký je medzi nimi rozdiel? Pri jednosmernom prúde prúdia elektróny stále jedným smerom a na zdroji je stále ten istý pól kladný a ten istý pól záporný. Vyrábajú ho chemické zdroje (klasické ,,baterky"). Pri striedavom prúde sa však póly zdroja vymieňajú (ten čo bol kladný, bude záporný a naopak), a teda elektróny prúdia raz na jednu stranu a raz na druhú. Vyrábajú ho elektrodynymické zdroje (dynamo, alternátor).

Pri striedavom prúde určujeme veličinu, ktorá sa volá frekvencia a jej jednotkou je hertz (Hz). Frekvencia vyjadruje, koľkokrát za sekundu za póly zdroja vymenia. V zásuvkách v Európe (a teda aj na Slovensku) je frekvencia 50Hz.

Striedavý prúd je v mnohých ohľadoch výhodnejší ako jednosmerný prúd: dajú sa pri ňom ľahko meniť hodnoty napätia a prúdu pri minimálnych stratách, pri jeho prenose na veľké vzdialenosti sú oveľa menšie straty ako pri jednosmernom prúde. Preto sa v elektrárňach vyrába striedavý prúd, ktorý sa transportuje aj do domácností. Ak nejaké zariadenie potrebuje pre svoje fungovanie jednosmerný prúd (napríklad počítač), obsahuje súčiastku, ktorá striedavý prúd zo zásuvky zmení na jednosmerný. Striedavý prúd je však zložitejšie učivo ako prúd jednosmerný, a tak sa na základnej škole o ňom veľa neučí.

Elektrické napätie

Elektrické napätie (U) je fyzikálna veličina s jednotkou volt (V). Je rovná práci, ktorú vykonajú elektrické sily zdroja pri presune náboja 1C medzi dvomi miestami obvodu. Čiže vlastne vyjadrujú akúsi ,,silu" alebo ,,námahu", ktorú musí zdroj na presun náboja vynaložiť.

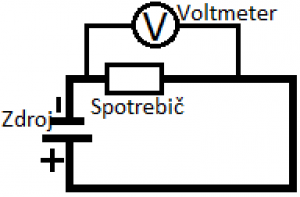
Napätie meriame voltmetrom. Keďže je definované (na rozdiel od prúdu) nie na určitom mieste (priereze) vodiča, ale medzi dvomi miestami vodiča, tak a voltmetrom ho musíme merať medzi dvomi miestami. Preto voltmeter zapájame do obvodu tzv. paralelne (vedľa seba), ako je na obrázku vpravo hore.

Napätie nezaťaženého zdroja sa nazýva elektromotorické napätie zdroja (U_e). Ak na zdroj napojíme spotrebič, napätie klesne. U niektorých zdrojov klesne len mierne (také zdroje sa nazývajú tvrdé, napríklad elektrická zásuvka) a u niektorých výraznejšie (také zdroje sa nazývajú mäkké, napríklad klasická baterka, hlavne takmer vybitá). V zásuvkách v Európe (a teda aj na Slovensku) je elektromotorické napätie 220 - 240 V.

Elektrický odpor

Ohmov zákon hovorí, že elektrický prúd je priamoúmerný elektrickému napätiu. Keď sa nad tým tak zamyslíme, je to logické, lebo čím väčšiu prácu vynaložíme, tým viac prúdu získame. Rozoberme si ale ten priamoúmerný vzťah. Rovnica priamej úmernosti je y=konštanta•x, v tomto prípade U=konštanta•I (vlastne platí aj, že I=konštanta•U, ale táto konštanta má inú hodnotu), z čoho si môžeme odvodiť, že ^U/_I=konštanta (ale aj ^I/_U=konštanta). Táto konštanta súvisí z elektrickými vlastnosťami daného vodiča, a nazýva sa elektrický odpor. Je to fyzikálna veličina so značkou R a jednotkou ohm [čítaj óm]. Značka ohmu je grécke písmeno Ω (omega). Používame aj iné jednotky, najčastejšie kiloohm (kΩ), ktorý elektrikári hovorovo nazývajú kilo. Vzorec pre výpočet odporu je R=^U/_I. Z toho si ľahko vieme odvodiť, že prúd vypočítame ako ^U/_R a napätie ako I•R.

Príčinou elektrického odporu (čiže prečo je elektrónom kladený odpor) je to, že elektróny narážajú do katiónov v kryštálovej mriežke kovu, a to ich brzdí.

Vyššie som uviedol, že platí aj závislosť I=konštanta•U a ^I/_U=konštanta. Touto konštantou je veličina, ktorá sa volá elektrická vodivosť. Jej značka je G a jej jednotkou je siemens (S). Je rovná prevrátenej hodnote elektrického odporu. Vodivosť sa používa oveľa menej ako odpor.

Vyrieš príklad (riešenie je na konci príspevku):

1.) Aký veľký prúd prechádza obvodom, ktorého odpor je 2 kΩ, ak je zapojený v zdroji s napätím 12V? Výsledok uveď v miliampéroch.

Závislosť elektrického odporu od vlastností vodiča

Elektrický odpor závisí od druhu, hrúbky, a dĺžky vodiča. Od dĺžky (l) závisí priamoúmerne (logicky, čím väčšiu vzdialenosť musí elektrón prekonať, tým viac katiónov bude mať v ceste) a od jeho hrúbky (obsahu prierezu, S) nepriamoúmerne (čím väčší obsah prierezu, tým viac priestoru elektrón má). Lenže dva rôzne kovy, hoci z rovnakou hrúbkou aj dĺžkou, nebudú mať rovnaký odpor. Preto bola pre každý kov nameraná veličina, ktorá sa nazýva rezistivita (merný odpor). Jej značkou je grécke písmeno ρ (ró). Odpor od nej závisí priamoúmerne. Vzorec pre odpor teda bude R=^ρ•l/_S. Z tohoto vzorca si pomocou klasických ekvivalentných úprav rovnice vieme odvodiť vzorec pre dĺžku (l=^R•S/_ρ), prierez (S=^ρ•l/_R) a rezistivitu (ρ=^R•S/_l).

Rezistivitu vieme pre každý materiál (pri bežných podmienkach, čiže pri izbovej teplote 20°C) nájsť vo fyzikálnych tabuľkách. Pokúsme sa odvodiť jej jednotku: už sme si odvodili, že vzorec pre rezistivitu bude ρ=^R^•S/_l. Dosadíme si do tohto vzorca jednotky odporu, obsahu a dĺžky (^Ω•m2/_m) a po pokrátení (^Ω•m2/_m) nám vyjde jednotka rezistivity Ωm (ohmmeter). Niekedy sa používa aj menšia jednotka rezistivity, Ωmm (ohmmilimeter).

Vyrieš príklady (riešenia sú na konci príspevku):

2.) Na výrobu rezistora (súčiastky s konštantným odporom, pozri nižšie) s odporom 10Ω chceme použiť odporový materiál chrómnikel, ktorého rezistivita je 1,1•10^-6Ωm. Chceme, aby mal tvar valca a aby jeho dĺžka bola 0,7cm. Aký hrubý musí byť? Výsledok uveď v milimetroch.

3.) Medzi koncami dvoma koncami drôtu je napätie 1,5V. Ampérmetrom sme v ňom namerali prúd 600mA. Aký dlhý je drôt, ak je obsah jeho prierezu 0,01mm² a je vyrobený z medi, ktorá má rezistivitu 1,7•10^-9Ωm?

Elektrický odpor však závisí aj od teploty. V kovoch elektrický odpor so zvyšujúcou sa teplotou mierne rastie. Je to hlavne preto, lebo pri zvýšenej teplote sa častice (teda aj katióny) budú viac pohybovať a ak sa katióny viac pohybujú, tak elektróny sa s nimi častejšie zrážajú, a to spôsobuje ich spomaľovanie. Naopak, pri nízkych teplotách bude odpor kovov nízky. V niektorých látkach sa môže stať, že keď ich schladíme na veľmi nízku teplotu, odpor úplne zmizne (bude sa rovnať nule). Tento jav sa nazýva supravodivosť a látky s takouto vodivosťou sa nazývajú supravodiče.

Lenže nielen zvýšená teplota spôsobuje väčší odpor, ale aj väčší odpor spôsobuje zvýšenú teplotu. Vyššie som uviedol, že v kovoch spôsobuje prechod elektrického prúdu zvýšenie teploty. Toto zvýšenie teploty je tým väčšie, čím väčší je aj odpor. Tento jav využívame v klasických žiarovkách. Prúd prechádza vodičom v žiarovke s veľkým odporom. Vodič v žiarovke sa prechodom prúdu zohreje na veľmi vysokú teplotu. Pri vysokých teplotách telesá začínajú vyžarovať svetlo, a tak aj vodič v žiarovke začne vydávať svetlo - žiarovka svieti. Hovorí sa, že žiarovku vynašiel Thomas Alva Edison. V skutočnosti však elektrické svetlo neobjavil, ale len prišiel na spôsob, ako ho spraviť využiteľným. V tej dobe vedci vedeli, že prechodom prúdu sa vodič rozsvieti. Vodiče, ktoré rozsvecovali, boli relatívne hrubé. Takéto svetlo sa nedalo využiť v praxi, lebo spotreba prúdu bola taká veľká, že každá žiarovka by potrebovala vlastnú malú elektrárničku. Edison však dostal nápad. Namiesto relatívne hrubých vodičov nechal prúd pretekať vláknom tenkým ako pavučinka. Tým rýchlo dosiahol vysoký odpor, a teda aj vysokú teplotu potrebnú na rozsvietenie. No nebolo to až také jednoduché. Tenké vlákna sa rýchlo ničili (vplyvom vysokej teploty sa roztopili, odparili alebo rozložili). Edison potreboval vlákno, ktoré znesie vysokú teplotu a svieti niekoľko sto hodín. Skúšal rôzne materiály, ale nájsť ten správny sa mu nedarilo.

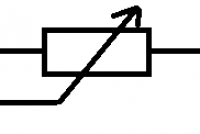
Nakoniec vyrobil vlákno zo zuhoľnatenej bavlnenej priadze. Vydržalo 40 hodín. Vlákno vyrobené zo zuhoľnateného kartónového papiera 170 hodín. Na Nový rok v noci v roku 1880 Edison rozsvietil svoje žiarovky pred davmi ľudí. Dnes sa ako vlákno do žiarovky používa wolfrámová špirála.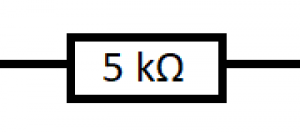

Rezistor, reostat a potenciometer

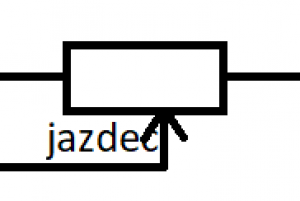
Rezistor je súčiastka s konštantným odporom. V elektrotechnike sa používa na dosiahnutie správneho odporu a prúdu v obvode. Schematická značka rezistora je zobrazená vpravo. Môžeme do nej vpísať aj hodnotu odporu, ktorý daný rezistor má. Na rezistor tiež zaznačujeme odpor. Pokiaľ má rezistor príliš malé rozmery na to, aby bola na ňom hodnota odporu napísaná, tak používame tzv. farebné značenie (každej kombinácii farebných pásikov zaznačených na rezistore prislúcha istá hodnota odporu).

Niekedy však chceme odpor meniť a nastavovať. Na to nám slúži súčiastky zvané reostat a potenciometer (rozdiel medzi nimi je vysvetlený nižšie). Obe tieto súčiastky fungujú n princípe posúvania jazdca po odporovej dráhe (ako je vyššie uvedené, čím väčšia dráha, tým väčší odpor). Reostat má dva vývody - jeden je jazdec a jeden je napevno zapojený. Naproti tomu potenciometer môže mať aj tri vývody (jeden jazdec a 2 napevno zapojené). Reostat je teda typ potenciometra, ktorý nemá jeden vývod zapojený. Schematická značka potenciometra (a teda aj reostatu) je zobrazená vpravo. Potenciometer vieme okrem regulácie prúdu v obvode využiť aj na delenie prúdu medzi vetvami v obvode (ak sa obvod rozvetvuje, pomocou potenciometra vieme regulovať, či pôjde viac prúdu do jednej vetvy alebo do druhej).

Niečo navyše

Skrat (spojenie nakrátko)

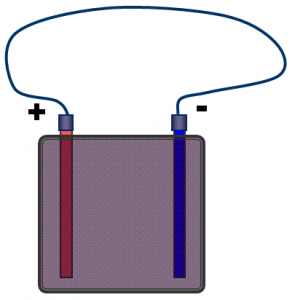Skrat (spojenie nakrátko), je situácia, keď je odpor vonkajšej časti obvodu takmer nulový (taký nízky, že ho zanedbávame). Takáto situácia nastane napríklad ak póly zdroja prepojíme vodičom, ale bez spotrebič alebo rezistora. Čo, samozrejme môžeme urobiť aj nechtiac, napríklad keď vytvoríme v obvode nežiaduci spoj.

Povedali sme si, že odpor zanedbávame, čiže ho považujeme za nulový. Aký bude potom prúd? Ak by sme ho chceli vypočítať tak, že napätie vydelíme odporom, museli by sme deliť nulou, čo nie je možné. Ako to teda vypočítame? Celý trik je v tom, že okrem vonkajšieho odporu (odpor všetkých vodičov, súčiastok a spotrebičov) existuje ešte aj vnútorný odpor. Celkový odpor obvodu sa rovná súčtu vonkajšieho a vnútorného odporu. Vnútorný odpor je oveľa menší ako vonkajší, a preto sme ho doteraz zanedbávali. Ale keď je vonkajší odpor nulový, vnútorný odpor začína zohrávať svoju rolu. Vnútorný odpor tvrdých zdrojov je menší ako vnútorný odpor mäkkých. V obvode bude pri skrate pretekať maximálny prúd (I_MAX), ktorý sa rovná podielu elektromotorického napätia zdroja a vnútorného odporu (keďže je celkový odpor rovný vnútornému, lebo vonkajší je nulový). Z toho sa okrem iného dá odvodiť, že vnútorný odpor sa dá vypočítať ako rozdiel elektromotorického napätia zdroja (napätia nezaťaženého zdroja) a svorkového napätia zdroja (napätia zaťaženého zdroja) vydelený odoberaným prúdom (R_i=^U_e-U/_I).

Zadanie: Napätie nezaťaženej autobatérie je 12,4V a pri odbere prúdu 40A sa zmenšilo na 11,2V. Určte vnútorný odpor batérie, maximálny prúd pri skrate a svorkové napätie pri odbere 60A.

Zápis:

Elektromotorické napätie (U_e)......................................12,4V
Svorkové napätie pri odbere I₁=40A (U₁)....................11,2V
Vnútorný odpor autobatérie (R_i)...................................?
Maximálny prúd pri skrate (I_MAX).................................?
Svorkové napätie pri odbere I₂=60A............................?

Výpočet:

Najprv si vypočítame vnútorný odpor autobatérie:

R_i=(U_e-U₁)/I₁=(12,4V-11,2V)/40A=1,2V/40A=0,03Ω

Potom si vypočítame maximálny prúd pri skrate:

I_MAX=U_e/R_i=12,4V/0,03Ω=400A

Nakoniec si vypočítame svorkové napätie pri odbere 60A. Vypočítame si to zo vzorca, ktorý sme si odvodili zo vzorca pre výpočet vnútorného odporu:

U₂=U_e-I₂•R_i=12,4V-60A•0,03Ω=12,4V-1,8V=10,6V

Odpoveď: Vnútorný odpor batérie je 0,03Ω, maximálny prúd pri skrate je 400A a svorkové napätie pri odbere 60A je 10,6V. Vnútorný odpor je 0,03Ω, čo je relatívne veľa. Takýto vysoký vnútorný odpor svedčí o buď o tom, že batéria je takmer vybitá, alebo že je už staršia a opotrebovanejšia.

Odber veľkých prúdov poškodzuje každý zdroj, okrem zdroja sa však kvôli zahriatiu na vysokú teplotu môže rozstaviť vodič kdekoľvek v obvode, a ak nám skrat nastane v elektrickom vedení v dome, v stenách sa nám ťažko bude hľadať poškodené miesto. Najväčšie nebezpečenstvo je riziko požiaru, keďže pre vysokú teplotu sa môže ,,chytiť" izolácia káblov a môže zapáliť omietky a ostatné predmety v dome. Skrat je preto nežiaduca situácia.

Na prevenciu pred týmito rizikami máme v dome ističe a poistky, ktoré odpoja zdroj, ak je prúd väčší ako povolená hodnota. To môže nastať nielen v prípade skratu, ale aj v prípade, že naraz používame viaceré spotrebiče, ktoré odoberajú vysoký prúd. Už sa vám asi stalo, že vám práve pre tento dôvod ,,vyhodilo poistky." No a ešte aký je rozdiel medzi poistkou a ističom. Poistka odpojí zdroj takým spôsobom, že keď ňou prejde vysoký prúd, ihneď sa vodič v nej rozstaví a nie je schopný prúd ďalej viesť. Poistka je teda zničená a musíme ju vymeniť. Na druhej strane, istič je vlastne klasický spínač, ktorý sa ale sám vypne, ak ním prejde vysoký prúd. Čiže ak ho ,,vyhodí", tak ho stačí len opätovne zapnúť. Väčšinou funguje na princípe elektromagnetu (obsahuje elektromagnet a elektromagnet vytvára silnejšie magnetické pole, ak ním prechádza vysoký prúd; ak ním prejde prúd väčší ako povolená hodnota, tak magnetické pole je dostatočne silné, aby ,,pritiahlo" spínač do vypnutej polohy).

Polovodiče

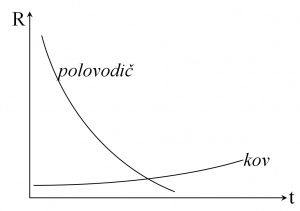Vyššie som napísal, že v kovoch (a platí to takmer pre všetky vodiče) elektrický odpor so zvyšujúcou sa teplotou mierne rastie (lebo pri zvýšenej teplote sa častice budú viac pohybovať a ak sa katióny viac pohybujú, tak elektróny sa s nimi častejšie zrážajú a to spôsobuje ich spomaľovanie). Existujú však látky, ktorých odpor pri zvýšenej teplote prudko klesá. Takéto látky sa nazývajú polovodiče. Príklady polovodičov sú kremík, germánium, selén, sulfid olovnatý, hemoglobín alebo chlorofil.

Prečo odpor polovodičov so zvyšujúcou sa teplotou prudko klesá? Vysvetlíme si to na príklade kremíka: Atómy kremíka majú na valenčnej vrstve 4 elekróny. Atómy každého prvku sa snažia zoskupovať tak, aby mali zaplnenú valenčnú vrstvu. Valenčná vrstva kremíka je zaplnená, ak má 8 elektrónov, takže kremík sa snaží získať ešte 4 ďalšie elektróny. Kremík je teda štvorväzbový, takže kryštálová mriežka kremíka vyzerá tak, že na každom kremíku sú naviazané 4 ďalšie, pričom dva susedné atómy majú vždy dva elektróny spoločné (pozri obrázok nižšie vľavo). Kremík teda v takomto prípade neobsahuje voľné elektróny, takže je izolant. Toto však platí len u chemicky čistého kremíka a pri nízkych teplotách. Ak teplotu zvýšime, dodáme elektrónom energiu a niektoré z nich sa uvoľnia z väzieb a stanú sa voľnými - kremík sa stane vodičom. Po elektróne zostane na väzbe prázdne miesto, ktoré má zdanlivý kladný náboj (spôsobený jadrami atómov). Toto miesto sa nazýva diera. Diery sú schopné zdanlivého pohybu. Deje sa to tak, že elektrón zo susednej väzby preskočí do diery a zaplní ju, ale ďalšia diera sa objaví na prázdnom mieste po elektróne, ktorý preskočil.


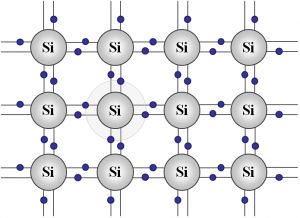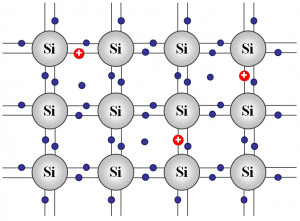Kremík pri nízkej teplote	Kremík pri zvýšenej teplote

Veľká závislosť odporu polovodičov od teploty sa využíva v súčiastke, ktorá sa volá termistor. Termistor je súčiastka, ktorá mení odpor v závislosti od teploty (schematická značka je vľavo). Termistor sa využíva napríklad na veľmi presné meranie teploty. Niektorým polovodičom možno meniť odpor aj iným dodaním energie, ako zvýšením teploty. Tento fakt využíva súčiastka s názvom fotorezistor, ktorá mení odpor v závislosti od množstva svetla, ktoré dostáva. Tiež je to veľmi užitočná súčiastka. využíva sa napríklad v automatickom osvetlení (ktoré svieti podľa toho, aká je tma), alebo vo fotobunkách.

Doteraz sme sa tu bavili o tzv. vlastných polovodičoch, ktoré tvoria chemicky veľmi čisté látky (aby kremík mohol byť vlastným polovodičom, musí mať čistotu 99,9999%). Čo sa však stane, ak je kremík znečistený?

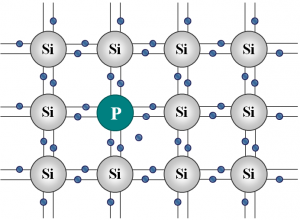
Ak sa v kryštálovej mriežke kremíka (ktorý má štyri valenčné elektróny) nachádza atóm zspiatimi (alebo viacerými) valenčnými elektrónmi (napríklad fosfor), na tvorbu väzieb z kremíkom použije 4 svoje elektróny a piaty ostáva voľný. Voľný elektrón môže zaplniť nejakú dieru. V kryštále teda ubudnú diery a pribudnú voľné elektróny. Polovodič, kde voľné elektróny dominujú nad dierami, sa nazýva polovodič typu N (z anglického ,,negative"-záporný).

Ak sa však v kryštálovej mriežke kremíka nachádza atóm s tromi (alebo menej) valenčnými elektrónmi, všetky tri svoje elektróny elektróny využije na tvorbu väzieb s kremíkom, a na jednej väzbe bude elektrón chýbať. Vznikne tam teda diera, ktorú však môže zaplniť voľný elektrón alebo elektrón zo susednej väzby. V kryštále teda ubudnú voľné elektróny a pribudnú diery. Diery sú však schopné zdanlivého pohybu (pozri vyššie), a tak bude takýto polovodič vodivý aj bez voľných elektrónov. Polovodič, kde diery dominujú nad voľnými elektrónmi, sa nazýva polovodič typu P (z anglického ,,positive"-kladný).

Polovodiče typu P aj polovodiče typu N nazývame nevlastné polovodiče.


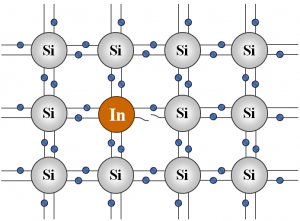Polovodič typu N	Polovodič typu P

Riešenia

1.) Zadanie: Aký veľký prúd prechádza obvodom, ktorého odpor je 2 kΩ, ak je zapojený v zdroji s napätím 12V? Výsledok uveď v miliampéroch. (Táto úloha je taká jednoduchá, že ani nepíšem zápis.)

Výpočet: I=^U/_R=^12V/_2000Ω=0,006A=6mA

Odpoveď: Obvodom prechádza prúd 6mA. Pre zaujímavosť, odpor ľudského tela je tiež 2kΩ, takže takýto prúd prechádza aj vami, keď sa napojíte na 12-voltovú baterku. Takýto malý prúd je úplne bezpečný.

2.) Zadanie: Na výrobu rezistora s odporom 10Ω chceme použiť odporový materiál chrómnikel, ktorého rezistivita je 112•10^-8Ωm. Chceme, aby mal tvar valca a aby jeho dĺžka bola 0,7cm. Aký hrubý musí byť? Výsledok uveď v milimetroch.

Zápis:

Odpor rezistora (R)................................10Ω
Rezistivita chrómnikla (ρ).....................1,1μΩm=1,1•10^-6Ω
Dĺžka rezistora (l)..................................0,7cm=7•10^-3m
Tvar prierezu.........................................kruh (keďže tvar rezistora je valec)
Obsah prierezu (S)...............................?
Hrúbka rezistora (r)..............................?

Výpočet:

Najprv si vypočítame obsah prierezu:

S=^ρ•l/_R=1,1•10^-6Ωm•7•10^-3m / 10Ω = 7,7•10^-10m²

Potom si zo vzorca pre výpočet obsahu kruhu (S= $\pi \,\!$ {\displaystyle \pi \,\!}r²) odvodíme vzorec pre výpočet jeho polomeru, ktorý si následne vynásobíme dvomi, aby sme dostali priemer:

r=√^S/_π=√(7,7•10^-10/3,14)≈1,6•10^-5m=1,6•10^-2mm=0,016mm

d=2•S=2•0,016mm=0,032mm

Odpoveď: Rezistor je hrubý 0,032mm (3,2•10^-2mm).

$\pi \,\!$ {\displaystyle \pi \,\!}

3.) Zadanie: Medzi koncami dvoma koncami drôtu je napätie 1,5V. Ampérmetrom sme v ňom namerali prúd 600mA. Aký dlhý je drôt, ak je obsah jeho prierezu 0,01mm² a je vyrobený z medi, ktorá má rezistivitu 1,7•10^-9Ωm?

Zápis:

Napätie medzi koncami drôtu (U)........................1,5V
Prúd v drôte (I).....................................................600mA=0,6A
Obsah prierezu drôtu (S).....................................0,01mm²=10^-8
Rezistivita medi (ρ)..............................................1,7•10^-9Ωm
Odpor drôtu (R)....................................................?
Dĺžka drôtu (l).......................................................?

Výpočet:

Najprv si vypočítame odpor drôtu:

R=^U/_I=^1,5V/_0,6A=2,5Ω

Potom si vypočítame dĺžku drôtu:

l=^R•S/_ρ=2,5Ω•10^-8mm² / 1,7•10^-9Ωm≈1,5•10¹m=15m

Odpoveď: Dĺžka drôtu je 15m.

(Späť k príkladom sa dostanete kliknutím na číslo príslušného príkladu.)

Rebelova škola doma

Menu

Elektrický prúd, napätie a odpor

Vyhľadávanie

Kontakt

Obľúbené odkazy