Rebelova škola doma

V elektrickom obvode máme 2 možnosti zapojenia dvoch súčiastok:

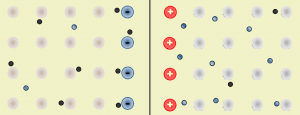
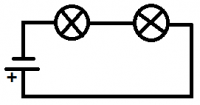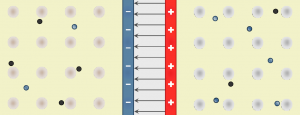
• Sériovo (za sebou) - súčiastky sú pekne za sebou jedna po druhej zapojené (pozri obrázok vpravo). Ak sa ktorákoľvek súčiastka v takomto zapojení poškodí, obvod už nie je uzatvorený, netečie ním prúd, a tak nefungujú ani ostatné spotrebiče. Kedysi bývali sériovo zapojené svetielka na vianočnom stromčeku. Keď sa nejaká žiarovka ,,vypálila" (čo sa stávalo skoro každý rok), prestali svietiť aj ostatné a ste museli pozorne prezrieť každú žiarovku, aby ste zistili, ktorá má prerušené vlákno (čiže, ktorá je ,,vypálená"), a teda ktorú treba vymeniť.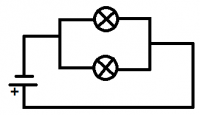
• Paralelne (vedľa seba) - v obvode sú uzly (uzol je miesto, kde sa stýkajú najmenej tri vodiče), kde sa vodič rozvetvuje, pričom v jednej vetve (vetva je časť obvodu medzi dvoma uzlami) je zapojená jedna súčiastka a v druhej vetve druhá (pozri obrázok vpravo).

V tomto príspevku budeme počítať prúd, napätie a odpor v sériových a paralelných zapojeniach, ako aj v ich kombináciách. Pri počítaní budeme zanedbávať odpor vodičov, lebo ten je naozaj veľmi malý.

Ak obvod obsahuje len sériové zapojenia (čiže nemá žiadne uzly), nazývame ho jednoduchý. Ak obvod obsahuje aj nejaké paralelné zapojenie (čiže má aspoň dva uzly), nazývame ho rozvetvený (zložený). Zložitý zložený elektrický obvod (má aj viac ako jeden zdroj) nazývame elektrická sieť.

Prúd, napätie a odpor v rôznych obvodoch

Sériové zapojenie elektrických spotrebičov

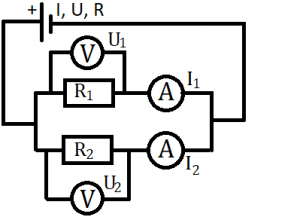
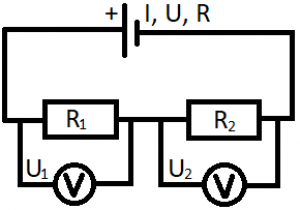Na ilustráciu použijeme príklad: Máme obvod, ktorého schéma je zobrazená na obrázku vľavo. Aký bude vzťah medzi celkovým odporom obvodu a odpormi jednotlivých spotrebičov, medzi prúdmi, ktoré prechádzajú spotrebičmi a celkovým prúdom, medzi napätím zdroja a napätiami jednotlivých spotrebičov? Je vcelku zrejmé, že keďže sa pri sériovom zapojení obvod nikde nevetví, prúd sa nemôže rozdeliť do jednotlivých vetiev, a tak bude v celom obvode rovnaký (I=const). Prišlo sa na to (ak samozrejme zanedbáme naozaj maličký odpor vodičov), že súčet odporov jednotlivých spotrebičov sa rovná celkovému odporu obvodu (R=R₁+R₂). Ako to bude s napätím? Keďže napätie je I•R, pričom I sa nemení a R sa sčítava, tak bude platiť, že elektromotorické napätie zdroja sa bude rovnať súčtu napätí jednotlivých spotrebičov (U=U₁+U₂). Keď si to zovšeobecníme, dostaneme tzv. 2. kirhoffov zákon: V jednoduchom uzavretom obvode (t.j. v časti obvodu, kde sú zdroje aj spotrebiče zapojené sériovo) sa súčet elektromotorických napätí zdrojov rovná súčtu úbytkov napätí.

Vyrieš príklad (riešenie je na konci príspevku):

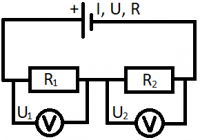1.) Máme daný obvod, ktorého schéma je zobrazená na obrázku vľavo. Svorkové napätie zdroja (U) je 4,5V. Odpor R₁ je 10 ohmov, odpor R₂ je 40 ohmov. Vypočítajte prúd prechádzajúci obvodom (I), celkový odpor (R) a napätie na svorkách jednotlivých spotrebičov (U₁, U₂).

Paralelné zapojenie jednotlivých spotrebičov

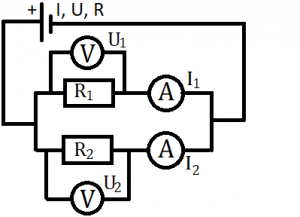Na ilustráciu použijeme príklad: Máme obvod, ktorého schéma je zobrazená na obrázku vľavo. Aký bude vzťah medzi celkovým odporom obvodu a odpormi jednotlivých spotrebičov, medzi prúdmi, ktoré prechádzajú spotrebičmi a celkovým prúdom, medzi napätím zdroja a napätiami jednotlivých spotrebičov? Opäť zanedbávame maličký odpor vodičov. Najprv si povieme vzťah pre napätie. Napätie bude v každej vetve rovnaké a bude sa rovnať svorkovému napätiu zdroja. Keďže prúd sa rozvetvuje do jednotlivých vetiev, tak celkový prúd obvodu sa rovná súčtu odporov jednotlivých spotrebičov (I=I₁+I₂). Keď si to zovšeobecníme, dotaneme tzv. 1. Kirfoffov zákon: Súčet prúdov, ktoré do uzla vstupujú sa rovná súčtu prúdov, ktoré z  neho vystupujú. Algebrický súčet (čiže ak prúdy vstupujúce do uzla považujeme za kladné a prúdy vystupujúce z uzla za záporné) všetkých prúdov v uzle dokopy sa rovná nule. Nakoniec si odvodíme celkový odpor. Vieme, že prúd sa sčítava a vypočítame ho podľa vzorca I=^U/_R. Z toho vyplýva, že ^U/_R=^U/_R1+^U/_R2. Keďže napätie je konštantné, môžeme ním danú rovnicu vydeliť a dostaneme vzorec: ¹/_R=¹/_R1+¹/_R2, čiže prevrátená hodnota celkového odporu sa rovná súčtu prevrátených hodnôt odporov jednotlivých spotrebičov. Klasickými ekvivalentnými úpravami rovnice si vieme odvodiť, že v prípade dvoch spotrebičov v obvode vypočítame celkový obvod podľa tohto vzorca: R=^R1•R2/_R1+R2. V prípade troch spotrebičov by ten vzorec vyzeral takto: R=^R1•R2•R3/_{R1•R2+R1•R3+R2•R3}.

Vyrieš príklady (riešenia sú na konci príspevku):

2.) Dva spotrebiče sú zapojené paralelne. Prvý z nich má odpor 20Ω a prechádza ním prúd 5A. Druhý má 100Ω. Aký prúd prechádza druhým spotrebičom, aký je celkový prúd a aké je napätie?

3.) Dva spotrebiče sú zapojené paralelne. Jeden z nich má odpor 60Ω a druhý 20Ω. Napätie je 12V. Aký prúd prechádza jednotlivými spotrebičmi a aký je celkový prúd a odpor?

Kombinácie sériového a paralelného zapojenia

Pri kombináciách sériového a paralelného zapojenia využívame, čo sme sa doteraz naučili. Príklady riešime tak, že postupne riešime rôzne časti obvodu a tak si ho zjednodušujeme. Napríklad ak máme v jednej vetve viac súčiastok so známym odporom, tak si ich odpory jednoducho spočítame a ďalej s vetvou už pracujeme tak, akoby tam bol len jeden rezistor s vypočítaným odporom.

Vyrieš príklady (riešenia sú na konci príspevku):

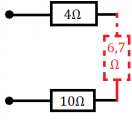
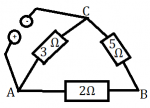
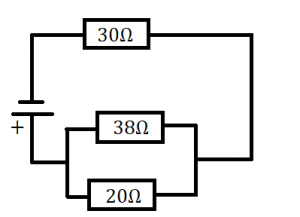4.) V obvode sú zapojené tri rezistory podľa schémy na obrázku vľavo. Napätie zdroja je 150V. Vypočítajte celkový odpor obvodu, celkový prúd a prúd v jednotlivých vetvách.

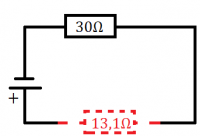
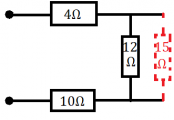
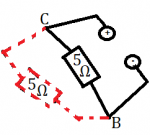
5.) Vypočítaj celkový odpor časti obvodu zobrazenej na nasledujúcom obrázku.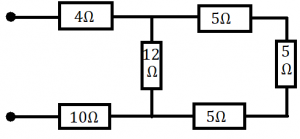

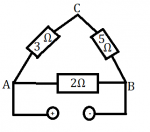
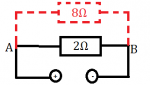
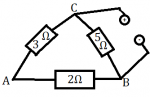
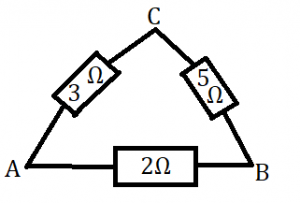6.) Aký bude celkový odpor obvodu zobrazenom na obrázku vľavo ak zdroj zapojím:

a) na vrcholy A a B?

b) na vrcholy B a C?

c) na vrcholy A a C?

Niečo navyše

Elektrické siete

Elektrická sieť  je rozvetvený elektrický obvod, v ktorom sa nachádza viac zdrojov. Pri počítaní s nimi využívame kirfoffove zákony. Zdroje musia byť zapojené tak, aby sa striedal kladný pól zo záporným, ináč by obvod nefungoval. A ako s tým počítame? Ukážeme si to na príklade:

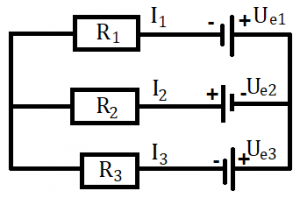Zadanie: Na obrázku vpravo je obvod. Elektromotorické napätie prvého zdroja (Ue1) je 8 voltov a tretieho zdroja (Ue3) 5 voltov. Odpor prvého rezistora (R1) je 2 ohmy, druhého rezistora (R2) 4 ohmy a tretieho rezistora (R3) 3 ohmy. Prúd v druhej vetve (I2) je 1 ampér. Vypočítajte prúdy v prvej a tretej vetve (I1, I3) a elektromotorické napätie druhého zdroja (Ue2).
Urobíme si zápis.	Ue1=8V        R1=2Ω        I1=? Ue2=?          R2=4Ω        I2=1A Ue3=5V        R3=3Ω        I3=?
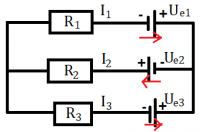
Začneme s výpočtom: 1. Zvolíme si smery prúdov. Podľa dohody vo vnútry zdrojov budú smerovať od záporného pólu ku kladnému a vo vonkajšej časti obvodu od kladného pólu k zápornému.
2. Zvolíme si smer obiehania v jednotlivých slučkách. Ten si volíme ľubovoľne, ale v každej slučke rovnako (buď všetky v smere hodinových ručičiek, alebo všetky proti smeru hodinových ručičiek).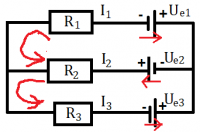
3. Pomocou kirhoffových zákonov si zostavíme a vyriešime sústavu rovníc. Ak smer prúdu nesúhlasí so smerom obiehania, tak daný prúd budeme odpočítavať.	I.   -I1-I2+I3=0    (1. kirhoffov zákon) II.  Ue1+Ue2=I1•R1+I2•R2    (2. zák.) III. Ue3+Ue2=I3•R3+I2•R2    (2. zák.) I.   I1=I3-I2=I3-1A II.  8V+Ue2=(I3-1A)•2Ω+1A•4Ω III. 5V+Ue2=I3•3Ω+1A•4Ω II.  8V+Ue2=I3•2Ω-2V+4V III. 5V+Ue2=I3*3Ω+4V II.  Ue2=I3•2Ω-6V III. 5V+I3•2Ω-6V=I3*3Ω+4V III. I3•2Ω-I3•3Ω=5V III. I3•(2Ω-3Ω)=5V III. I3•(-1Ω)=5V    =>I3=-5A I.   I1=I3-1A=-5A-1A=-6A II. Ue2=I3•2Ω-6V=-5A•2Ω-6V=-16V
Zapíšeme odpoveď.	Prúd v prvej vetve (I1) je -6V a prúd v tretej vetve (I3) je -5A. Elektromotorické napätie druhého zdroja (Ue2) je -16V.

Diódový jav

Ak kladnú svorku zdroja pripojíme k polovodiču typu P a zápornú svorku k polovodiču typu N, tak elektrické pole prechodu PN sa účinkom elektrického poľa zo zdroja napätia zoslabí. Voľné elektróny a diery prejdú do oblasti prechodu a odpor prechodu sa tak zmenší. Elektrickým obvodom teda prechádza prúd a preto hovoríme, že prechod PN je zapojený v priepustnom smere.

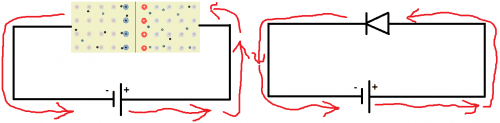
Ak kladnú svorku zdroja pripojíme k polovodiču typu N a zápornú svorku k polovodiču typu P, tak elektrické pole  prechodu PN sa účinkom elektrického napätia zo zdroja napätia zosilní. Odpor prechodu sa tak podstatne zmenší. Obvodom prechádza iba veľmi malý prúd tvorený iba menšinovými voľnými časticami (tzv. záverný prúd) a preto hovoríme, že prechod PN je zapojený v závernom smere.

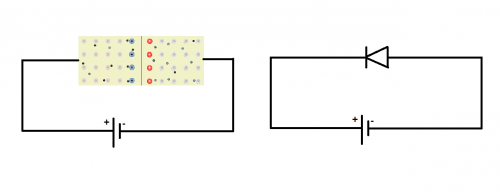
Závislosť elektrického odporu polodvodiča s prechodom PN od polarity vonkajšieho zdroja napätia pripojeného k polovodiču nazývame diódový jav. Polovodič s prechodom PN nazývame polovodičová dióda. Dióda sa využíva, keď chceme prúd usmerniť, čiže viesť len jedným smerom v rozvetvenom obvode. Takisto sa využíva na premenu striedavého prúdu na jednosmerný.

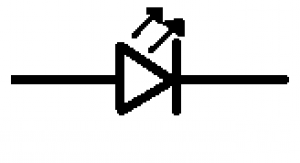
Keď elektrón v dióde zapojenej v priepustnom smere prejde prechodom a zaplní dieru, jeho energia sa zníži (keďže bude zastabilizovaný). Keďže sa jeho energia zníži, tak v zmysle zákona zachovania energie sa nejaká energia musí vypustiť von. To sa v dióde deje jej vyžiarením vo forme elektromagnetického vlnenia. Vlnová dĺžka vyžiareného elektromagnetického vlnenia závisí najmä od druhu prímesových atómov v polovodičoch, z ktorých sa dióda skladá. Pri správnej kombinácii týchto atómov vieme dosiahnuť, aby dióda vyžiarila viditeľné svetlo. Tak sme vyrobili svetelnú (luminiscenčnú) diódu. Označujeme ju LED (z anglického light-emitting diode). Takéto ,,ledky" majú rôznorodé využitie. Keďže oproti klasickým žiarovkám majú nízku spotrebu energie, tak sa vyžívajú v kontrolkách, úsporných lampách, displejoch, atď.

Riešenia

(Späť k príslušnému príkladu sa dostanete kliknutím na jeho číslo)